PAST QUESTIONS 2011

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Take the test

---

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

---

Question 1

1. In a school of 255 students, 80 of them study Arabic only and 125 study French only. Each student studies at least one of the two subject.

   \(\hspace{0.5cm} i)\) Draw a Venn diagram to represent the information.

   \(\hspace{0.5cm} ii)\) How many students study

   \(\hspace{1cm} \alpha)\) both subjects?

   \(\hspace{1cm} \beta)\) French?

   Show Solution

   Question

   
   
   

2. Make \(h\) the subject of \(v = \frac{1}{3}\pi r^2h\).

   Show Solution

   Question

   
   
   

3. A bookseller bought 80 copies of books at \(GH₵3.50\) per copy. He sold each of them at \(GH₵4.20\). Find

   \(\hspace{0.5cm} i)\) the total cost price;

   \(\hspace{0.5cm} ii)\) his percentage profit.

   Show Solution

   Question

   
   
   

---

Question 2

1. The pie chart below shows the distribution of exercise books to six schools \(A, B, C, D, E\) and \(F\) in a town. School \(D\) was given \(8,000\) exercise books.

   

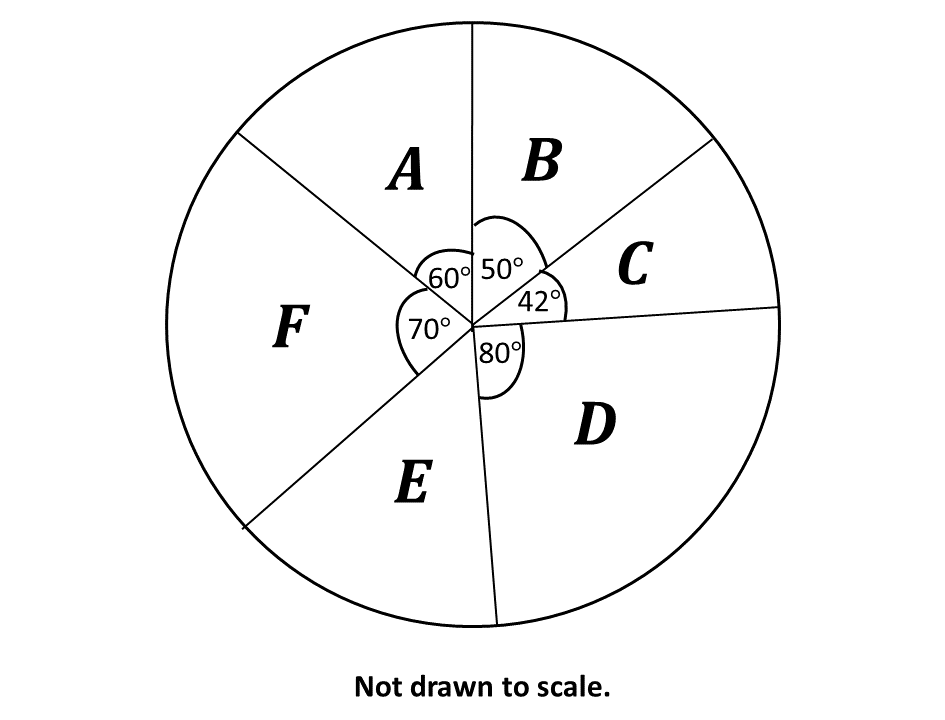
   \(\hspace{0.5cm} i)\) How many exercise books were given to each of the rest of the schools?

   \(\hspace{0.5cm} ii)\) What is the average number of exercise books given to the schools?

   \(\hspace{0.5cm} iii)\) How many schools had less than the average number of exercise books?

   Show Solution

   Question

   
   
   

2. Solve the inequality below and illustrate the answer on the number line.

   \(\hspace{0.5cm}\) \(\frac{1}{3}x + 1 \geq \frac{1}{2}x + \frac{1}{4}(2 - x)\)

   Show Solution

   Question

   
   
   

---

Question 3

1. Using a ruler and a pair of compasses only, construct

   \(\hspace{0.5cm} i)\) triangle \(ABC\) such that \(|AB| = 8\) cm, angle \(CBA = 45^\circ\) and angle \(CAB = 60^\circ\).

   \(\hspace{0.5cm} ii)\) the bisector of angle \(ACB\) to meet \(|AB|\) at \(T\).

2. Measure

   \(\hspace{0.5cm} i)\) \(|CT|\);

   \(\hspace{0.5cm} ii)\) angle \(CTB\)

   Show Solution

   Question

   
   
   

3. A boy spent \(\frac{3}{8}\) of his money and had Gh₵15.00 left. How much did he have?

   Show Solution

   Question

   
   
   

---

Question 4

1. The perimeter of a rectangular plot of land whose length is \((2x + 5)\) m and width \((x - 5)\) m is 80 m. Find the

   \(\hspace{0.5cm} i)\) value of \(x\);

   \(\hspace{0.5cm} ii)\) area of the plot;

   \(\hspace{0.5cm} iii)\) cost of weeding the plot at Gh₵0.24 per m\(^2\).

   Show Solution

   Question

   
   
   

2. Find the value of \(x\) and \(w\) in the diagram below if \(|AB| = |BC|\).

   
   Show Solution

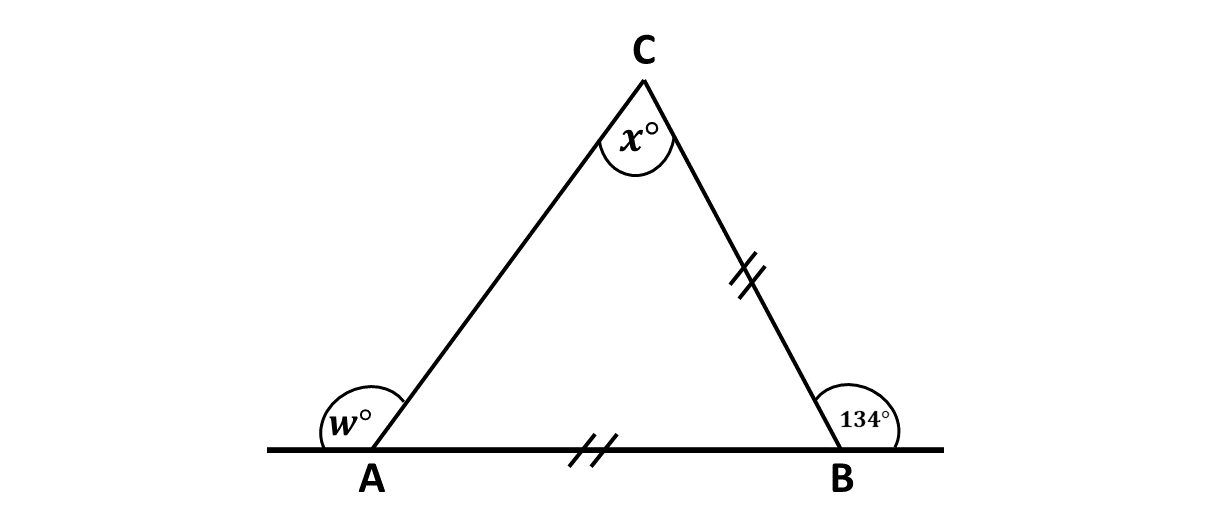
   Question

   
   
   

---

Question 5

1. \(a)\) Given that \(\mathbf{a} = \begin{pmatrix}-3 \\ 3 \end{pmatrix}\) and \(\mathbf{b} = \begin{pmatrix}4 \\ -6 \end{pmatrix}\)

   calculate

   \(\hspace{0.5cm} i)\) \(\mathbf{a} + 2\mathbf{b}\)

   \(\hspace{0.5cm} ii)\) \(\frac{1}{2}(2\mathbf{a} - \mathbf{b})\)

   Show Solution

   Question

   
   
   

2. The number of pupils in a primary school is given in the table below:

   

   \(\hspace{0.5cm} i)\) Find the number of pupils in the school.

   \(\hspace{0.5cm} ii)\) What is the mean number of pupils in a class?

   \(\hspace{0.5cm} iii)\) What percentage of pupils are in class six?

   Show Solution

   Question

   
   
   

3. Convert \(312_{five}\) to a base ten numeral.

   Show Solution

   Question

   
   
   

---

Question 6

1. Copy and complete the table below for the relation \(y = \frac{x}{20}\), where \(y\) is the cost (in Ghana cedis) and \(x\) is the weight (in grammes) of rice sold in a market.

   

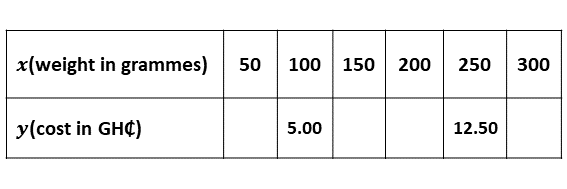
2. \(i)\) On a graph sheet, draw two perpendicular axes \(OX\) and \(OY\)

   \(\hspace{0.5cm} ii)\) Using a scale of 2 cm to 50 grammes on the \(x\)-axis and 2 cm to Gh₵2.00 on the \(y\)-axis draw the graph of the relation \(y = \frac{x}{20}\).

3. Using the graph, find

   \(\hspace{0.5cm} i)\) the cost of 175 grammes of rice;

   \(\hspace{0.5cm} ii)\) the weight of rice that can be bought with Gh₵14.00.

   Show Solution

   Question

   
   
   

---