PAST QUESTIONS 2015

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Take the test

---

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

---

Question 1

1. In class of 70 students, 40 belong to the Red Cross Society, 27 belong to the Girls' Guide Society and 12 belong to both the Red Cross Society and the Girls' Guide Society. The remaining students do not belong to any of the two societies.

   \(\hspace{0.5cm}i)\) Illustrate the information on a Venn diagram.

   \(\hspace{0.5cm}ii)\) How many students belong to the Red Cross Society only?

   \(\hspace{0.5cm}iii)\) How many students do not belong to any of the two societies?

2. A farmer uses \(\frac{1}{3}\) of his land to plant cassava, \(\frac{2}{5}\) of the remaining land to plant maize and the rest vegetables. If vegetables cover an area of 10 acres, what is the total area of the farmer's land?

---

Question 2

1. Solve for \(x\), if \(2 - \frac{3}{5}x \leq 1\frac{1}{3}\)

2. At a rally attended by 520 people, 30% were Fantes, 25% Ewes, 15% Nzemas, 20% Gas and the rest Gonjas.

   \(\hspace{0.5cm} i)\) How many Gonjas were at the rally?

   \(\hspace{0.5cm} ii)\) How many more Fantes than Nzemas were at the rally?

   \(\hspace{0.5cm} iii)\) Draw a pie chart to illustrate the information?

---

Question 3

1. Mr. Mensah's farm is 20 km from his house. He uses his car to travel \(y\) km of the distance from his house and then walks \(1\frac{1}{2}\) hours at the rate of 3 km per hour to get to his farm. Find \(y\).

2. The perimeter of a square field is the same as that of a rectangular field. If the length of the rectangular field is 8 km and the width is 5 km, calculate the area of the square field.

3. Find the gradient of the line which passes through the points \(M(2, -1)\) and \(K(-3, 6)\).

---

Question 4

1. Using a ruler and a pair of compasses only, construct triangle \(PST\) with angle \(PST = 30^\circ\), \(|ST| = 9\) cm and \(|PS| = 12\) cm.

2. With \(T\) as the center, draw a circle of radius \(6\) cm.

3. Construct the perpendicular bisector (mediator) of line \(PS\).

4. Label the intersection of the circle and the mediator \(Q_1\) and \(Q_2\).

5. \(i)\) Measure \(|Q_1Q_2|\).

   \(ii)\) Measure angle \(Q_1TQ_2\).

---

Question 5

1. Anita bought 51 tubes of yam at 3 for Gh₵10.00. If she sold them and made a loss of 40%, how much did she sell each tuber of yam?

2. The volume of a cylinder closed at one end is 1056 cm\(^3\). If its height is 21 cm, find its:

   \(\hspace{0.5cm} i)\) diameter

   \(\hspace{0.5cm} ii)\) total surface area.

---

Question 6

1. \(i)\) Copy and complete the following mapping:

   

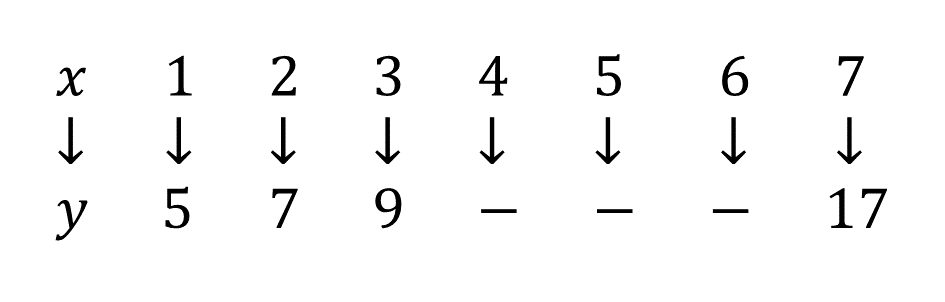
   \(\hspace{0.5cm} ii)\) Determine the rule for the mapping.

2. Draw two perpendicular axes \(Ox\) and \(Oy\) on a graph sheet.

3. Using a scale of 2 cm to 1 unit on the \(x\)-axis and 2 cm to 2 units on the \(y\)-axis, mark the \(x\)-axis from \(0\) to \(8\) and the \(y\)-axis from \(0\) to \(20\).

4. Plot the point for each ordered pair \((x, y)\) and join them with a straight line.

5. Find:

   \((i)\) \(y\) when \(x\) is 0.

   \((ii)\) \(x\) when \(y\) is 14.

---