PAST QUESTIONS 1992

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Take the test

---

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

---

Question 1

1. Solve $5 - 2x > x + 2$, where $x$ is a real number.

   Illustrate your result on the number line.

   Show Solution

   Question 1. $a$

   $5 - 2x > x + 2$

   $\Rightarrow -2x - x > 2 -5$

   $\Rightarrow \hspace{0.6cm} -3x > -3$

   $\Rightarrow \hspace{0.6cm} \dfrac{-3x}{-3} < \dfrac{-3}{-3}$

   $\Rightarrow \hspace{1cm} x < 1$

   $\therefore$ {$x:x < 1, \ x$ is a real number}

   
   

   Illutrating on the number line:

   
   
   

   ---

   
   
   
   
   

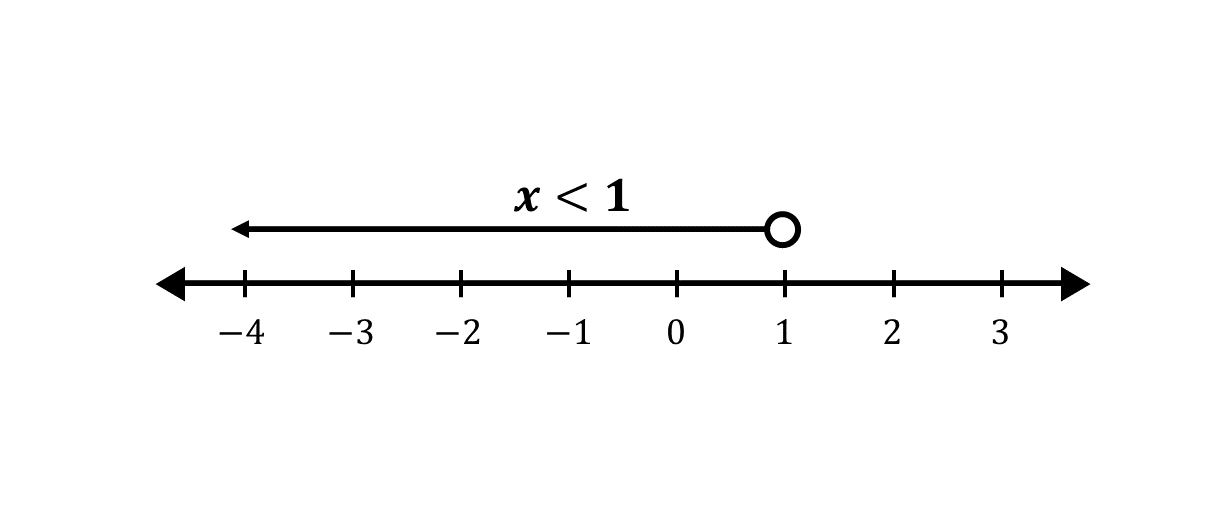
2. Find the truth set of the equation:

   $\frac{2}{3}(3y - 1) - (y + 2) = \frac{1}{3}$

   Show Solution

   Solution

   $\frac{2}{3}(3y - 1) - (y + 2) = \frac{1}{3}$

   Multiplying through by the L.C.M of 3

   $\Rightarrow 3(\frac{2}{3}(3y - 1)) - 3(y + 2)$$= 3(\frac{1}{3})$

   $\Rightarrow 2(3y - 1) - 3(y + 2) = 1$

   $\Rightarrow 6y - 2 - 3y - 6 = 1$

   $\Rightarrow 6y - 3y - 2 - 6 = 1$

   $\Rightarrow \hspace{1.3cm} 3y - 8 = 1$

   $\Rightarrow \hspace{1.88cm} 3y = 1 + 8$

   $\Rightarrow \hspace{1.88cm} 3y = 9$

   $\Rightarrow \hspace{1.76cm} \dfrac{3y}{3} = \dfrac{9}{3}$

   $\Rightarrow \hspace{2.1cm} y = 3$

   $\therefore y$ is 3

   Hence, the truth set of the equation is $\{y:y = 3\}$.

   
   
   

   ---

   
   
   
   
   

3. Factorise completely: $mp + np - mt - nt$

   Show Solution

   Solution

   $mp + np - mt - nt$

   $\Rightarrow (mp + np) - (mt + nt)$

   $\Rightarrow p(m + n) - t(m + n)$

   $\Rightarrow (m + n)(p - t)$

   
   
   

   ---

   
   
   
   
   

4. Make $t$ the subject of the relation $v = u + at$

   Show Solution

   Solution

   $v = u + at$

   Making $t$ the subject

   $\Rightarrow v - u = at$

   $\Rightarrow \dfrac{v - u}{a} = \dfrac{at}{a}$

   $\Rightarrow \dfrac{v - u}{a} = t$

   Re-arranging the relation

   $\Rightarrow t = \dfrac{v - u}{a}$

   
   
   

   ---

   
   
   
   
   

---

Question 2

A landlady rented out her house for ₵ 240,000.00 for one year. During the year, she paid 15% of the rent as income tax. She also paid 25% of the rent as property tax and spent ₵ 10,000.00 on repairs. Calculate

1. The landlady's total expenses.

Show Solution

Question 2$a$

Amount gotten $= ₵ 240,000.00$

Amount spent on income tax

$\Rightarrow 15\% \ \ of \ \ ₵ 240,000.00$

$\Rightarrow \dfrac{15}{100} \times ₵ 240,000.00$

$\Rightarrow 15 \times ₵ 2400$

$\Rightarrow ₵ 36,000.00$

Amount spent on property tax

$\Rightarrow 25\% \ \ of \ \ ₵ 240,000.00$

$\Rightarrow \dfrac{25}{100} \times ₵ 240,000.00$

$\Rightarrow 25 \times ₵ 2400$

$\Rightarrow ₵ 60,000.00$

Amount spent on repairs

$\Rightarrow ₵ 10,000.00$

Total expense = income tax + property tax + repairs

Hence, Total expense

$\Rightarrow$$₵ 36,000.00 +$$₵ 60,000.00 +$$₵ 10,000.00$

$\Rightarrow$$₵ 106,000.00$

$\therefore$ the landlady's total expense was $₵ 106,000.00$





---







2. The remainder of the rent after the landlady's expenses.

Show Solution

Question 2$b$

Amount gotten $= ₵ 240,000.00$

Total expense $= ₵ 106,000.00$

Remaining amount $=$ Amount gotten $-$ total expense

Hence, Remaining amount $= ₵ 240,000.00 -$$₵ 106,000.00$

$\Rightarrow$ Remaining amount $= ₵ 134,000.00$

$\therefore$ she had $₵ 134,000.00$ remaining after her expenses.





---







3. The percentage of the rent she spent on repairs.

Show Solution

Question 2$c$

Percentage spent on repairs.

$\Rightarrow \dfrac{amount \ on \ repairs}{amount \ gotten} \times 100\%$

$\Rightarrow \dfrac{₵10,000}{₵240,000} \times 100\%$

$\Rightarrow \dfrac{1}{24} \times 100\%$

$\Rightarrow \dfrac{100}{24}\%$

$\Rightarrow \dfrac{4 \times 25}{4 \times 6}\%$

$\Rightarrow \dfrac{25}{6}\%$

$\Rightarrow 4.1667\%$

$\therefore$ percentage of rent spent on repairs is $4.1667\%$





---

---

Question 3

1. Using a scale of 2cm to 1 unit on both axes, draw two perpendicular lines $OX$ and $OY$ on a graph sheet.

2. On this graph sheet, mark the $x-$axis from $-5$ to $5$ and the $y-$axis from $-6$ to $6$.

3. Plot on the same graph sheet the points $A(1, 1)$, $B(4, 3)$ and $C(2, 5)$. Join the points $A, B$ and $C$ to form a triangle.

4. Using the $y$-axis as mirror line, draw the image of the triangle $ABC$ such that $A \rightarrow A^\prime$, $B \rightarrow B^\prime$ and $C \rightarrow C^\prime$.

5. Using the $y$-axis as the mirror line, draw the image of triangle $ABC$ such that $A \rightarrow A^{\prime\prime}$, $B \rightarrow B^{\prime\prime}$ and $C \rightarrow C^{\prime\prime}$.
   Write down the coordinates of $A^{\prime\prime}$, $B^{\prime\prime}$ and $C^{\prime\prime}$.

Show Solution

---

Question 4

The table below gives the frequency distribution of the marks obtained in a class test by a group of 64 pupils.

1. Draw a bar chart for the distribution.

Show Solution

Solution

Question 4$(a)$






---







2. A pupil is chosen at random from the class, what is the probability that the pupil obtained 7 marks?

Show Solution

Solution

Question 4$(b)$


Total number of pupils:
$\Rightarrow 9 + 14 + 13 + 10 + 5 + 8 + 2 + 3$
$\Rightarrow 64$

Pupils who obtained 7 marks $= 8$


Probability $= \dfrac{successful \ outcomes}{total \ outcomes}$

Prob.(obtaining 7 marks):

$\Rightarrow \dfrac{8}{64}$

$\Rightarrow \dfrac{1\times 8}{8 \times 8}$

$\Rightarrow \dfrac{1}{8}$

$\therefore$ the probability of choosing a pupil who obtained 7 marks is $\frac{1}{8}$.





---

---

Question 5

1. Using a ruler and a pair of compasses only:

2. Draw $|PQ|=9cm$

3. Construct a perpendicular to $PQ$ at $Q$

4. Construct $\angle QPS = 60^\circ$ at the point $P$ on $PQ$ such that $PS = 6.5 cm$

5. Construct a line parallel to $PS$ through $S$. Let the perpendicular through $Q$ and the parallel through $S$ meet at $R$. Measure $|PR|$

Show Solution

---