PAST QUESTIONS 1994

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Take the test

---

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

---

Question 1

1. Multiply \((a - b)\) by \((2b - a)\)

Show Solution

Question 1a

\((a - b)(2b - a)\)

\(\Rightarrow a(2b - a) - b(2b - a)\)

\(\Rightarrow 2ab - a^2 - 2b^2 + ab\)

\(\Rightarrow 2ab + ab - a^2 - 2b^2\)

\(\Rightarrow 3ab - a^2 - 2b^2\)





---








2. Find the truth set of \(2x - 6 \le 5(3 - x)\)
   Illustrate your answer on a number line.

Show Solution

Question 1b

\(2x - 6 \le 5(3 - x)\)

\(\Rightarrow 2x - 6 \le 15 - 5x\)

\(\Rightarrow 2x + 5x\le 15 + 6 \)

\(\Rightarrow \hspace{0.8cm} 7x \le 21 \)

dividing both sides by the coefficient

\(\Rightarrow \hspace{0.8cm} \dfrac{7x}{7} \le \dfrac{21}{7} \)

\(\Rightarrow \hspace{1cm} x \le 3 \)

\(\therefore\) the truth set is \(\{x:x \le 3\}\).





Illustrating on the number line





---








3. Given that \(\mathbf{u}=\begin{pmatrix}-2 \\ 3 \end{pmatrix}\) and \(\mathbf{v}=\begin{pmatrix}2 \\ 6 \end{pmatrix}\), find \(\frac{1}{3}\left( \mathbf{u}+\frac{1}{2}\mathbf{v} \right)\).

Show Solution

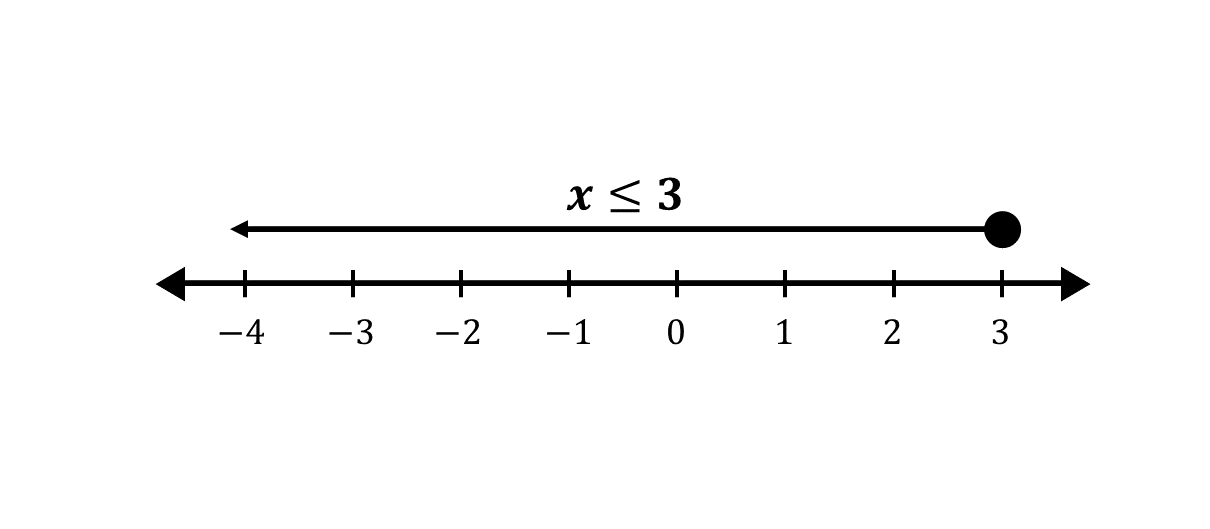
Question 1c

\(\mathbf{u}=\begin{pmatrix}-2 \\ 3 \end{pmatrix}\)

\(\mathbf{v}=\begin{pmatrix}2 \\ 6 \end{pmatrix}\)

Hence, \(\frac{1}{3}\left( \mathbf{u}+\frac{1}{2}\mathbf{v} \right)\)

\(\Rightarrow \frac{1}{3}\begin{pmatrix} \begin{pmatrix}-2 \\ 3 \end{pmatrix} + \frac{1}{2}\begin{pmatrix}2 \\ 6 \end{pmatrix} \end{pmatrix}\)

\(\Rightarrow \frac{1}{3}\begin{pmatrix} \begin{pmatrix}-2 \\ 3 \end{pmatrix} + \begin{pmatrix}1 \\ 3 \end{pmatrix} \end{pmatrix}\)

\(\Rightarrow \frac{1}{3}\begin{pmatrix} -2 + 1 \\ 3 + 3 \end{pmatrix}\)

\(\Rightarrow \frac{1}{3}\begin{pmatrix} -1 \\ 6 \end{pmatrix}\)

\(\Rightarrow\) \( \begin{pmatrix} -\frac{1}{3} \\ 2 \end{pmatrix} \)





---

---

Question 2

1. A ladder leans against a wall. The end of the ladder touches the wall 12 m from the ground. The foot of the ladder is 9 m away from the foot of the wall.

   \(\hspace{0.5cm} (i)\) What is the length of the ladder?

   \(\hspace{0.5cm} (ii)\) Calculate the angle that the ladder makes with the ground.

   Show Solution

   Solution

   
   

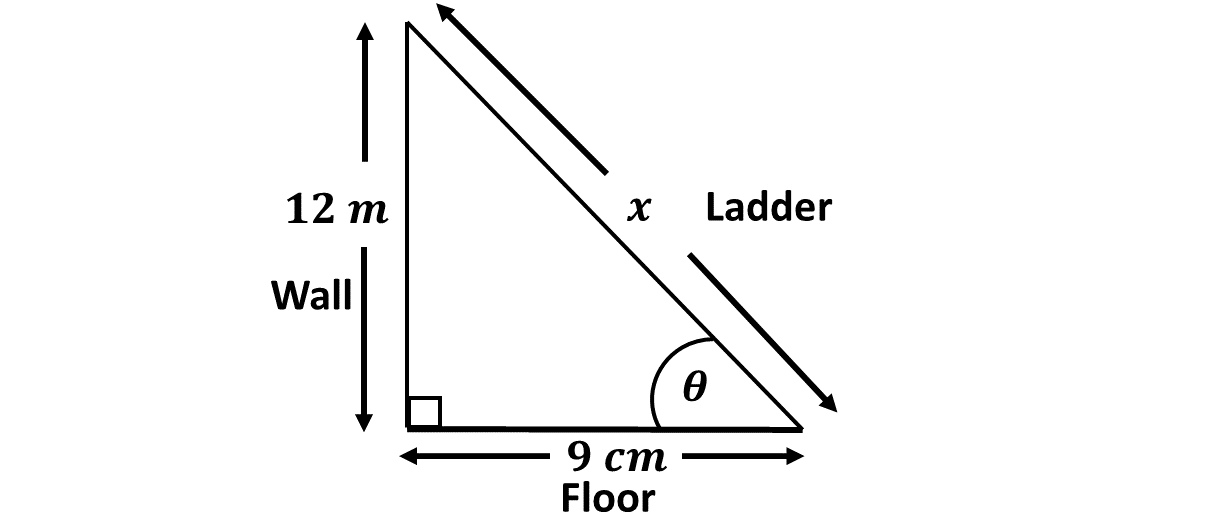
   Question 2a.i

   Length of wall = 12 m
   Distance from foot to wall = 9 m
   Let the length of the ladder = \(x\)
   

   Using Pythagoras theroem:

   \(\Rightarrow x^2 = 12^2 + 9^2\)
   \(\Rightarrow x^2 = 144 + 81\)
   \(\Rightarrow x^2 = 225\)
   \(\Rightarrow x = \sqrt{225}\)
   \(\Rightarrow x = \sqrt{15^2}\)
   \(\Rightarrow x = 15\) m
   \(\therefore\) the ladder is 15 m long.

   
   
   

   Question 2a.ii

   let the angle = \(\theta\)

   \(\Rightarrow tan \ \theta = \dfrac{opp}{adj}\)

   \(\Rightarrow tan \ \theta = \dfrac{12}{9}\)

   \(\Rightarrow tan \ \theta = \dfrac{3 \times 4}{3 \times 3}\)

   \(\Rightarrow tan \ \theta = \dfrac{4}{3}\)

   \(\Rightarrow \theta = tan^{-1}\left(\frac{4}{3}\right) \)

   \(\therefore\) the angle is \(tan^{-1}\left(\frac{4}{3}\right) \)

   
   
   

   ---

   
   
   
   
   



2. Given that \(\pi = 3.14\) and \(g = 20\), find the value of \(F\) in the Relation \(F = \dfrac{3\pi g^2}{4}\)

Show Solution

Solution

\(\pi = 3.14\)

\(g = 20\)

\(F = \dfrac{3\pi g^2}{4}\)

Substituting \(\pi\) and \(g\) into the equation:

\(\Rightarrow F = \dfrac{3 \times 3.14 \times 20^2}{4}\)

\(\Rightarrow F = \dfrac{9.42 \times 400}{4}\)

\(\Rightarrow F = \dfrac{9.42 \times 4 \times 100}{4}\)

\(\Rightarrow F = 9.42 \times 100\)

\(\Rightarrow F = 942\)

\(\therefore F\) is \(942\)





---

---

Question 3

Using a ruler and a pair of compasses only;

1. Construct triangle \(PQR\) in which \(|PQ| =\) 8 cm, \(\angle QPR = 45^\circ\) and \(\angle PQR = 90^\circ\). Measure \(|QR|\).

2. Construct the mediator of \(PQ\) to meet \(PR\) at the point \(S\). With \(S\) as center and radius 3 cm, construct a circle.

Show Solution

Solution





---

---

Question 4

Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular lines \(Ox\) and \(Oy\) on a graph sheet, mark the \(x-\)axis from \(-5\) to \(5\), and \(y-\)axis \(-6\) to \(6\). Mark the origin \(O\).

\((i)\) Draw on the same graph sheet indicating in each case the coordinates of all vertices of the square \(ABCD\) where \(A(1, 2)\), \(B(4, 2)\), \(C(4, 5)\) and \(D(1, 5)\) are the respective points.

\((ii)\) Using the \(y-\)axis as a mirror line draw the image \(A_1B_1C_1D_1\) of square \(ABCD\) where \(A \rightarrow A_1\), \(B \rightarrow B_1\), \(C \rightarrow C_1\), \(D \rightarrow D_1\)

\((iii)\) Draw the enlargement \(A_2B_2C_2D_2\) of the square with scale factor \(-1\) from \(O\), such that \(A \rightarrow A_2\), \(B \rightarrow B_2\), \(C \rightarrow C_2\), \(D \rightarrow D_2\).

\((iv)\) What single tranformation maps \(A_2B_2C_2D_2\) to \(A_1B_1C_1D_1\)?

Show Solution

---

Question 5

The following shows the distribution of sales of soft drinks sold by Jatokrom JSS canteen in one week.

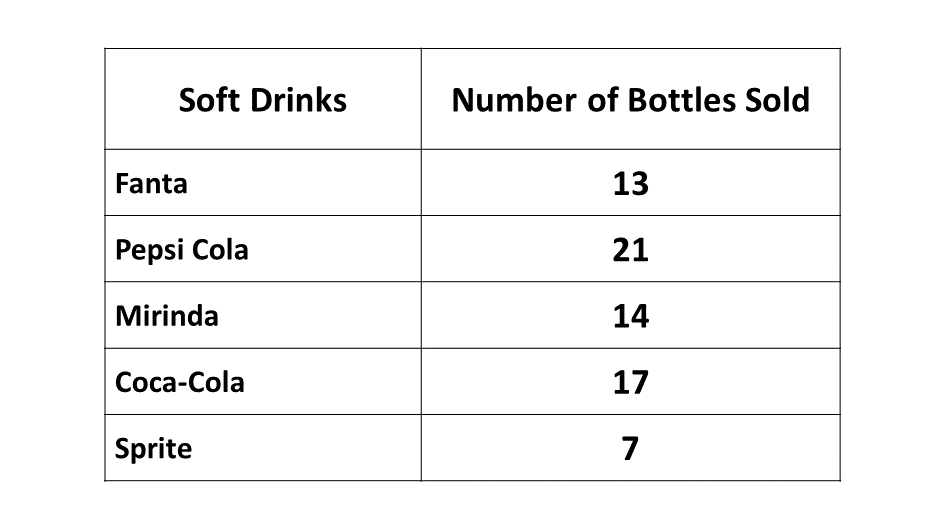
Draw a pie chart to illustrate the sales.

Show Solution

---