PAST QUESTIONS 2020

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Kindly contact the administrator of the site on WhatsApp or Phone (0208711375) for the link to the test.

---

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

---

Question 1

1. If \(M =\) {Prime integers between \(1\) and \(11\)} and \(N =\) {factors of 12}, find:

   \((i)\) \(M \cup N\)

   \((ii)\) \(M \cap N\)


Show Solution

Solution




2. Simplify \(45 \div 3 + 2 \times 8 - 12 + 42\)

Show Solution

Solution




3. 

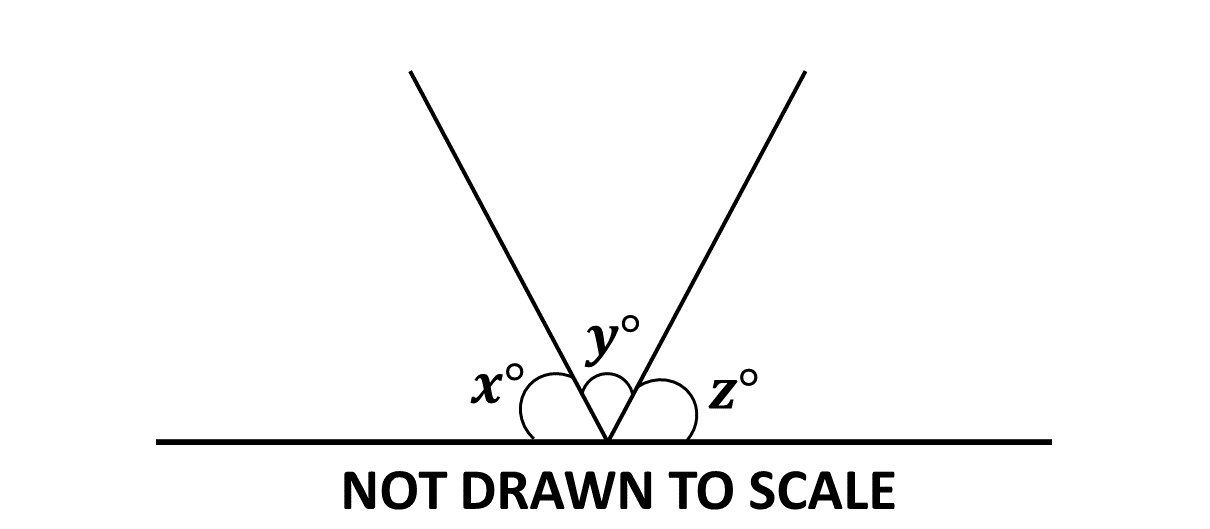
In the diagram, \(x, y\) and \(z\) are angles on a straight line. If \(x^\circ : z^\circ = 2 : 3\), and \(y = 80^\circ\), find \(x\).


Show Solution

Solution

---

Question 2

1. Simplify: \(5(6 - ab) + 2(-7 + 3ab)\)


Show Solution

Solution





2. The equation of a straight line is given by \(3x - 2y - 6 = 0\). Find the:

   \((i)\) gradient of the line;

   \((ii)\) y-intercept.


Show Solution

Solution





3. Adwoa received a commission of 20% on bread she sold. In one week, Adwoa's commission was Gh₵ 540.00.

   \((i)\) How much bread did she sell during that week?

   \((ii)\) Find her average daily commission.


Show Solution

Solution

---

Question 3

1. Express \((\frac{13}{15} - \frac{7}{10})\) as a percentage.


Show Solution

Solution





2. Factorize: \(ay - y - a + 1\).


Show Solution

Solution





3. In a fishing community of 9,400 people, the number of women exceeds the number of men by 1,500. Find the ratio of men to women in the community.


Show Solution

Solution

---

Question 4

1. Solve: \(\frac{2x + 3}{3} + 2x = 10\)


Show Solution

Solution





2. Multiply 0.03858 by 0.02, leaving the answer in standard form.


Show Solution

Solution





3. A cylindrical container of height 28 cm and diameter 18 cm is filled with water. The water is then poured into another container with a rectangular base of length 27 cm and width 11 cm. Calculate the depth of the water in the container. [Take \(π = \frac{22}{7}\)]


Show Solution

Solution

---

Question 5

1. If \(11y = (18)^2 - (15)^2\), find the value of \(y\).


Show Solution

Solution





2. Find the perimeter of a circle with radius 35 cm. [Take \(\pi = \frac{22}{7}\)]


Show Solution

Solution





3. Given that \(m = \frac{r - s}{2nr}\)

   \((i)\) make \(r\) the subject of the relation.

   \((ii)\) find the value of \(r\) when \(s = 117, m = 2\) and \(n = -3\).


Show Solution

Solution

---

Question 6

1. Copy and complete the table for the relation \(y = 12x - 9\)

   

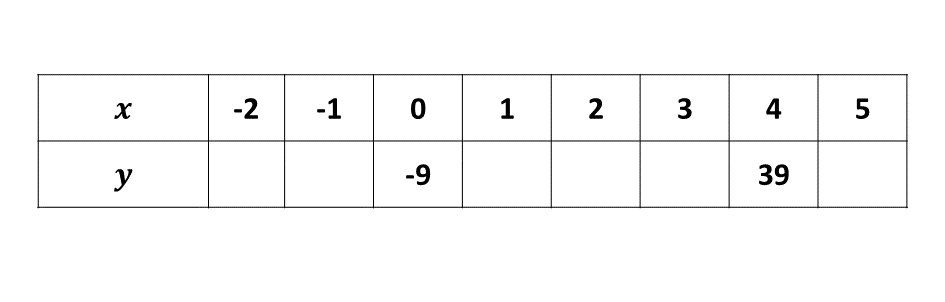
   \((i)\) Using a scale of 2 cm to 1 unit on the \(x\) - axis and 2 cm to 10 units on the \(y\) - axis, draw on a graph sheet two perpendicular axes \(Ox\) and \(Oy\).

   \((ii)\) Using the table, plot all the points of the relation \(y = 12x - 9\) on the graph.

   \((iii)\) Draw a straight line through the points.

   \((iv)\) Use the graph to find:

   \(\hspace{0.5cm} (\alpha)\) \(y\) when \(x = 2.5\);

   \(\hspace{0.5cm} (\beta)\) \(x\) when \(y = 10\);


Show Solution

Solution





2. List the integers within the interval \(7 < x \leq 14\)


Show Solution

Solution

---