BECE

Year to Practice:
1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002A 2002B 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023 2024

PAST QUESTIONS 2003


Section A

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.





Section B

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.





Question 1


    \(ξ\) = {1, 2, 3, 4, ..., 18};

    \(A\) = {Prime numbers} and

    \(B\) = {Odd numbers greater than 3}

  1. If \(A\) and \(B\) are subsets of the universal set, \(ξ\), list the members of \(A\) and \(B\).

  2. Find the set

    \((i)\) \(A \cap B\)
    \((ii)\) \(A \cup B\)

  3. \((i)\) Illustrate \(ξ\), \(A\) and \(B\) on a Venn diagram

    \((ii)\) Shade the region for prime factors of 18 on the Venn diagram.


    4. Solution









Question 2


  1. If \(2n - 5m + 10 = 0\), find

    \((i)\) \(m\), when \(n = 2\)

    \((ii)\) \(n\), when \(m = 5\)

    2. Solution







  2. Simplify \(\frac{6.4 \times 0.25 \times 16}{0.8 \times 0.5}\) leaving your answer in standard form.

    3. Solution







  3. A number of sweets were shared among 8 children and each child received 30. If 12 children shared the same number of sweets, how many will each receive?

    4. Solution









Question 3


    The table shows the distribution of the ages (in years) of children in a nursery school.

    The table as described above.

  1. Find

    \((i)\) the modal age

    \((ii)\) the mean age.

  2. Draw a bar chart for the distribution.

  3. What is the probability that a child chosen from the school is 4 years old?

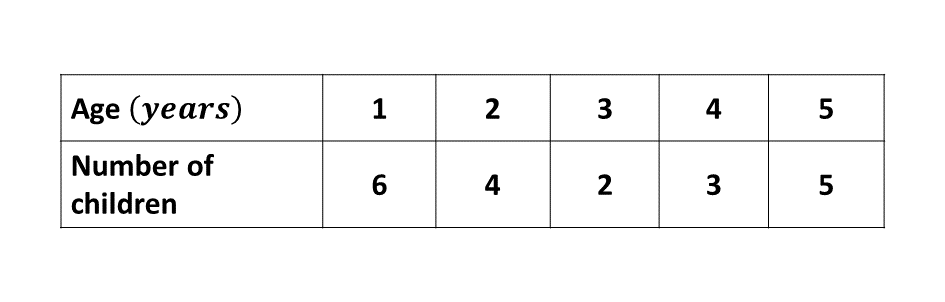
    4. Solution









Question 4


  1. If \(\mathbf{p} = \begin{pmatrix}4 \\ 5 \end{pmatrix}\), \(\mathbf{q} = \begin{pmatrix}0 \\ -2 \end{pmatrix}\) and \(\mathbf{r} = \begin{pmatrix}-3 \\ 7 \end{pmatrix}\),

    Find \(\mathbf{p} + 2\mathbf{q} + \mathbf{r}\)

    2. Solution







  2. Find the solution set of the inequality \(x - \frac{4}{5} \leq \frac{1}{5}\), if the domain is the set \(\{-2, -1, 0, 1, 2\}\)

    3. Solution







  3. A rectangular sheet of metal has length 44 cm and breadth 10 cm. It is folded to form a cylinder with the breadth becoming the height. Calculate

    \((i)\) the radius of the cylinder formed;

    \((ii)\) the volume of the cylinder.

    [Take \(\pi = \frac{22}{7}\)]

    4. Solution











Question 5


  1. Using a pair of compasses and a ruler only,

    \(\hspace{0.5cm} i)\) Construct the triangle \(ABC\) with \(|AB| = 8\) cm, \(|BC| = 8\) cm and \(|AC| = 7\) cm.

    \(\hspace{0.5cm} ii)\) Bisect \(ABC\) and let the bisector meet \(AC\) at \(D\). Produce \(|BD|\) to \(P\) such that \(|BD| = |DP|\). Join \(AP\) and \(CP\).

    2. Solution











To advertise on our website kindly call on 0208711375 or 0249969740.

SHS JHS PRI 4 - 6 PASSCO