BECE
Year to Practice:
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002A
2002B
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
2015
2016
2017
2018
2019
2020
2021
2022
2023
2024
PAST QUESTIONS 2007
Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.
Click on the link below when you are ready.
Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.
Question 1
-
In a class of 39 students, 19 offer French and 25 offer Ga. Five students do not offer any of the two languages. How many students offer only French?
-
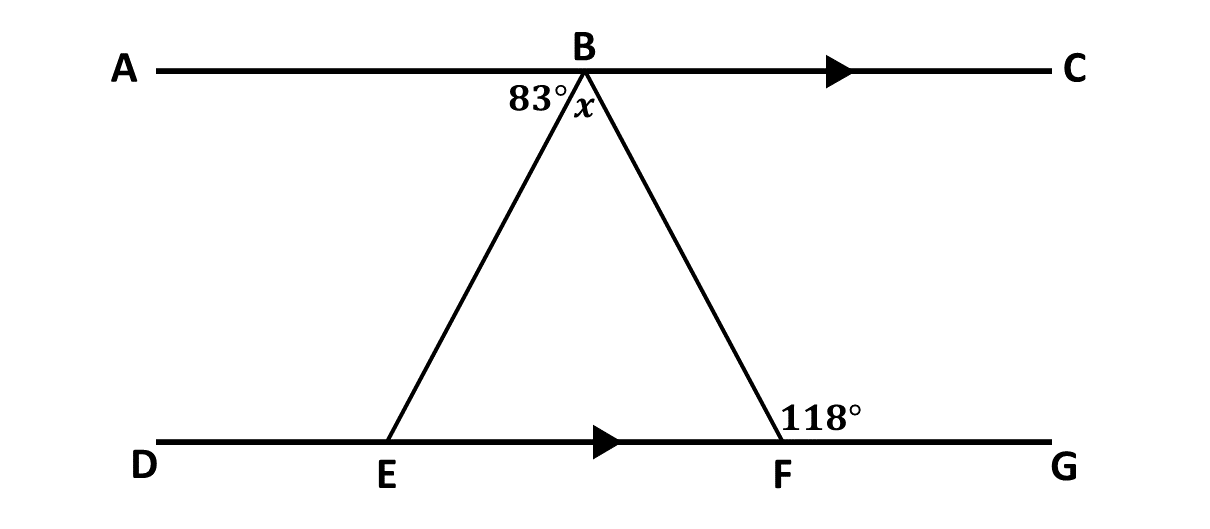
In the diagram above, \(AC\) is parallel to \(DG\), angle \(BFG = 118^\circ\) and angle \(ABE = 83^\circ\). Find the value of
\(\hspace{0.5cm} (i)\) angle \(CBF\)
\(\hspace{0.5cm} (ii)\) \(x\)
-
A fair die is thrown once.
\(\hspace{0.5cm} (i)\) Write down the set of all the possible outcomes.
\(\hspace{0.5cm} (ii)\) Find the probability of obtaining a multiple of 2.
\(\hspace{0.5cm} (iii)\) What is the probability of obtaining a prime number?
Question 2
-
A water tank in the form of a cuboid of height 22cm and a rectangular base of length 7cm and width 5cm is filled with water. The water is then poured into a cylindrical container of diameter 14cm. Calculate the height of the water in the cylindrical container. (Take \(\pi = \frac{22}{7}\))
-
A trader is given 15 percent discount on goods bought from a factory. If the original price of an item in the factory is ₵45,000,000.00, calculate
\(\hspace{0.5cm} (i)\) the discount on the item
\(\hspace{0.5cm} (ii)\) the amount the trader paid for the item.
-
Find the truth set of \(\frac{x - 3}{3} \leq \frac{1}{2} + x\) and illustrate your answer on the number line.
Question 3
-
Construct triangle \(PQR\) such that the length of \(PQ = 10\) cm, angle \(QPR = 90^\circ\) and angle \(PQR = 30^\circ\).
\(\hspace{0.5cm}\)Measure the length of \(PR\).
-
Bisect the angle \(QRP\) to meet \(PQ\) at \(M\).
-
With \(M\) as center, and radius \(MP\) draw a circle.
-
Measure the radius of the circle.
Using a ruler and a pair of compasses only,
Question 4
-
\((i)\) Write down the frequency table for the distribution.
\((ii)\) Use the table to find the mean mark.
-
If the pass mark is 4, how many pupils failed the test?
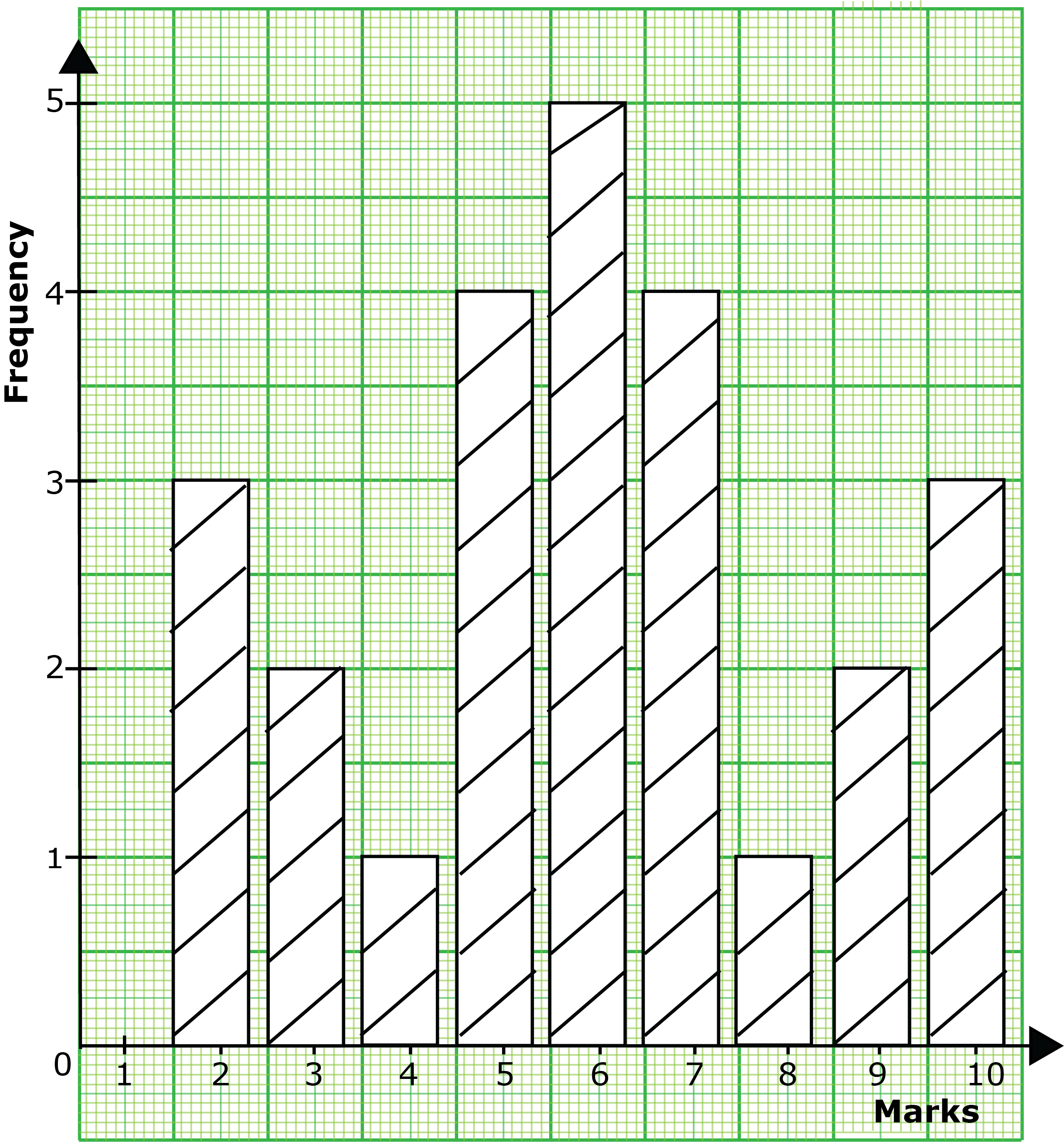
The bar chart above is for the distribution of marks in a class test.
Question 5
-
Mr Jones used 173 units of electricity last month. If the charge for the first 110 units was ₵150 per unit and ₵200 per unit for the rest, calculate the total bill for Mr. Jones.
-
Express 4 hours in seconds leaving your answer in standard form.
-
Given the vectors \(\mathbf{r} = \begin{pmatrix}3 \\ -5\end{pmatrix}\) and \(\mathbf{p} = \begin{pmatrix}-7 \\ -9\end{pmatrix}\), and \(\mathbf{q} = 2\mathbf{p} - \mathbf{r}\), find \(\mathbf{q}\)
Question 6
-
Using a scale of 2 cm to 2 units on both axes, draw two perpendicular axes \(Ox\) and \(Oy\) on a graph sheet. On the same graph sheet, mark the \(x\)-axis from \(-10\) to \(10\) and the \(y\)-axis from \(-10\) to \(10\).
\((i)\) Plot \(A(2, 2)\), \(B(6, 2)\) and \(C(4, 6)\). Join \(AB\), \(BC\) and \(AC\).
\((ii)\) Draw the image triangle \(A_1B_1C_1\) of triangle \(ABC\) under a clockwise rotation of \(90^\circ\) about the origin, where \(A \rightarrow A_1\), \(B \rightarrow B_1\) and \(C \rightarrow C_1\).
\((iii)\) Draw the image triangle \(A_2B_2C_2\) of triangle \(ABC\) under a reflection in the \(y-\)axis, where \(A \rightarrow A_2\), \(B \rightarrow B_2\) and \(C \rightarrow C_2\).
-
When 12 is added to a certain number and the sum is multiplied by 4, the result is 60. Find the number.
For sponsorship or advertisement kindly call or whatsapp on 0208711375 or 0249969740.