PAST QUESTIONS 1995

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Take the test

---

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

---

Question 1

1. There are 20 students in a hostel, 16 of them are fluent in French and 10 of them are fluent in English. Each student is fluent in at least one of the languages.

   \((i)\) Illustrate the information on a Venn diagram.

   \((ii)\) How many students are fluent in both English and French?

Show Solution

Question \(1a (i)\)

let \(\mathbf{U} =\) students in the hostel

let \(F =\) students fluent in French

let \(E =\) students fluent in English

\(n(U) = 20\)

\(n(F) = 16\)

\(n(E) = 10\)

let \(n(F \cap E) = x\)





---





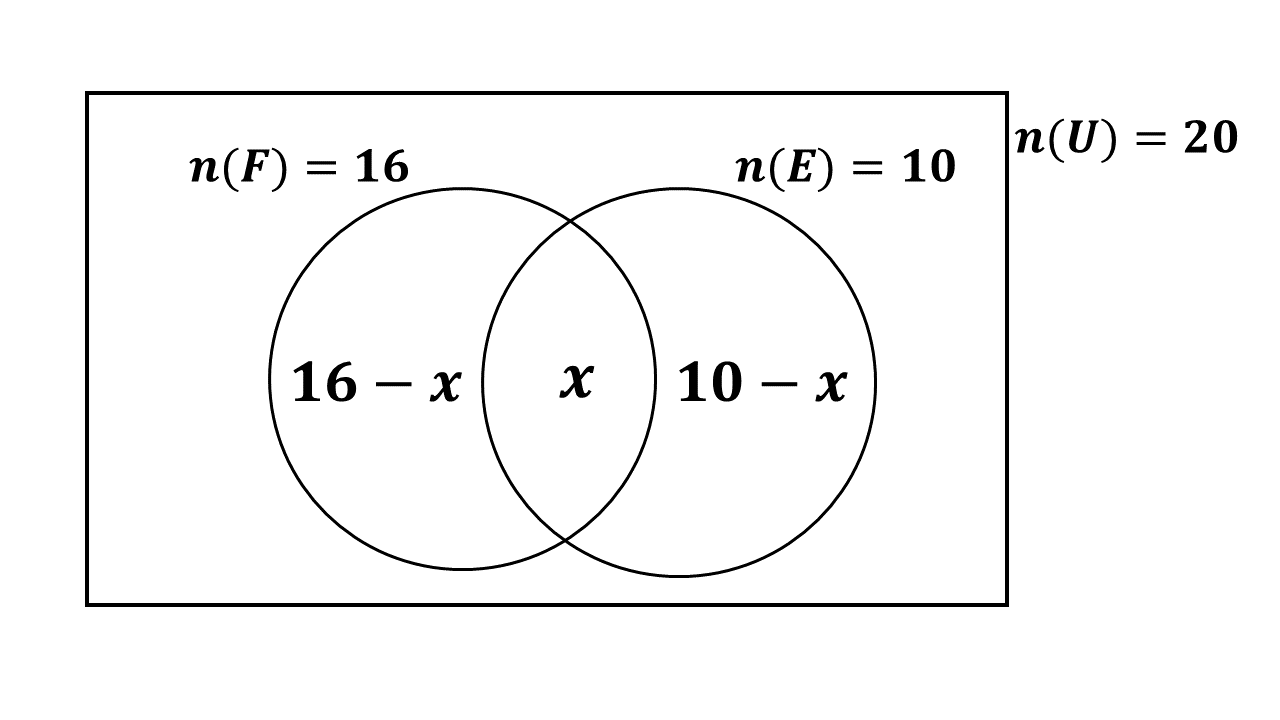
Question \(1a (ii)\)

From the Venn diagram,

\(\Rightarrow 16 - x\) \(+\) \(x\) \(+\) \(10 - x\) \(=\) \(20\)

\(\Rightarrow 16\) \(+\) \(10 - x\) \(=\) \(20\)

\(\Rightarrow 26 - x\) \(=\) \(20\)

\(\Rightarrow -x\) \(=\) \(20 - 26 \)

\(\Rightarrow -x\) \(=\) \(-6 \)

\(\Rightarrow \dfrac{-x}{-1}\) \(=\) \(\dfrac{-6}{-1} \)

\(\Rightarrow x\) \(=\) \(6\)

\(\therefore\) 6 students speak both French and English fluently.





---








2. The sum of ages of two brothers Kofi and Kweku is 35. Kofi's age is two-thirds Kweku's age. Find their ages.

Show Solution

Solution

Let Kweku's age \(= x\)

\(\therefore\) Kofi's age \(\Rightarrow \frac{2}{3}\) of \(x\)

\(\hspace{1.7cm} \Rightarrow \frac{2}{3}\)\(x\)

Sum of their ages:

\(\Rightarrow x + \frac{2}{3}x = 35\)

Multiplying through by the L.C.M of 3

\(\Rightarrow 3x + 3(\frac{2}{3}x) = 3 \times 35\)

\(\Rightarrow 3x + 2x = 105\)

\(\Rightarrow 5x = 105\)

\(\Rightarrow \frac{5x}{5} = \frac{105}{5}\)

\(\Rightarrow x = 21\)

\(\therefore\) Kweku is \(21\) years old




Kofi's age \(\Rightarrow \frac{2}{3}x \)

\(\Rightarrow \frac{2}{3} \times 21 \)

\(\Rightarrow 2 \times 7\)

\(\Rightarrow 14\)

\(\therefore\) Kofi is \(14\) years old





---

---

Question 2

1. Using a ruler and a pair of compasses only,

   \((i)\) Construct a triangle \(ABC\) such that \(|AB| = 9\) cm, angle \(BAC = 60^\circ\) and angle \(ABC = 45^\circ\).

   \((ii)\) Construct a line from the point \(C\) perpendicular to \(AB\) and let it meet \(AB\) at \(P\). Measure \(|CP|\) and \(|AP|\).

2. What is the value of angle \(ACP\)?

Show Solution

Solution





---

---

Question 3

1. Mansah earns a salary of ₵10,000.00 per month as a sales girl. In addition to the salary, she is given a commission of 1.5% of whatever sales she makes in a month. In January, this year, she made sales of ₵7,500,000.00. What is the total amount Mansah earned at the end of January?

Show Solution

Solution

Her monthly salary = ₵10,000.00
Her January sales = ₵7,500,000.00
Monthly commission = \(1.5 \%\) of her sales


January commission:

\(\Rightarrow\) \(1.5 \% \) of ₵\(7,500,000.00 \)

\(\Rightarrow\) \(\dfrac{1.5}{100} \times\) \(7,500,000 \)

\(\Rightarrow\) \( 1.5 \times\) \(75000 \)

\(\Rightarrow\) \( 1.5 \times\) \(75 \times 1000 \)

\(\Rightarrow\) \( 1500 \times 75 \)

\(\Rightarrow\) \( 112,500 \)

\(\therefore\) her commission for January was ₵112,500.00

Total earning for January:

\(\Rightarrow\) Monthly salary + Commission

\(\Rightarrow 10,000 + 112,500 \)

\(\Rightarrow 122,500 \)

\(\therefore\) her total earning for January was ₵122,500.00





---








2. The diagram below shows a circle with center O and radius 14cm.

   

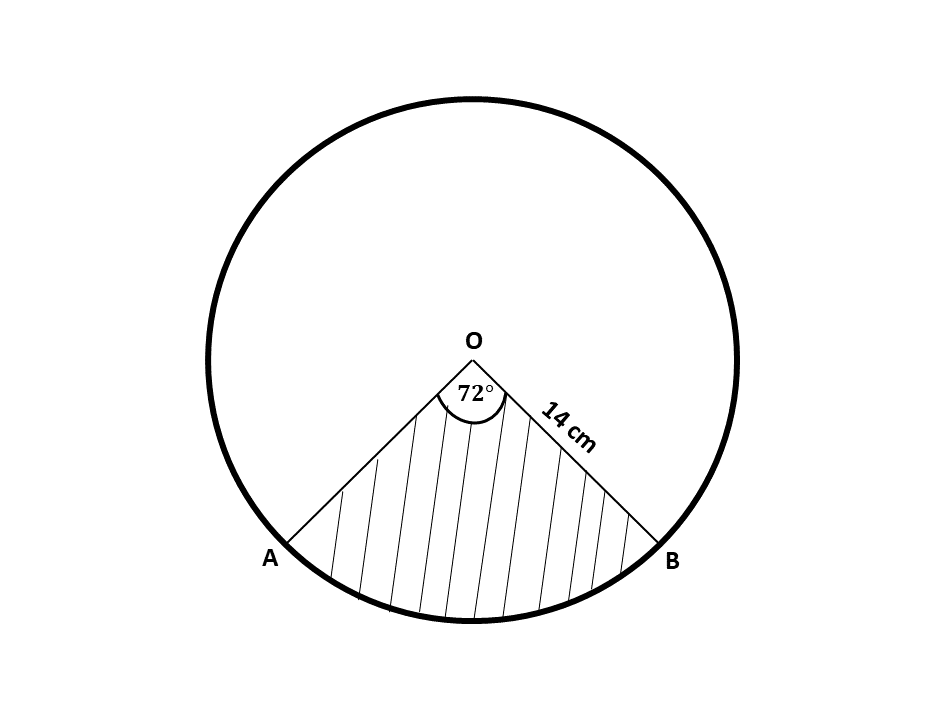
   The shaded region \(AOB\) is a sector with angle \(AOB = 72^\circ\). Find

   \((i)\) the length of the minor arc \(AB\)

   Show Solution

   Question 3\(b. i.\)

   radius, \(r = 14\) cm

   \(\theta = 72^\circ\)

   Length of minor arc:

   \(\Rightarrow \dfrac{\theta}{360^\circ} \times 2\pi r\)

   \(\Rightarrow \dfrac{72^\circ}{360^\circ} \times 2 \times \dfrac{22}{7} \times 14 \ cm\)

   \(\Rightarrow \dfrac{1}{5} \times 2 \times 22 \times 2 \ cm\)

   \(\Rightarrow \dfrac{88}{5} \ cm\)

   \(\Rightarrow 17.6 \ cm\)

   \(\therefore\) the length of the minor arc is 17.6 cm

   
   
   

   ---

   
   
   
   
   

   \((ii)\) the area of the shaded sector \(AOB\)

   [Take \(\pi = \frac{22}{7}\)]

   Show Solution

   Question 3\(b. ii.\)

   radius, \(r = 14\) cm

   \(\theta = 72^\circ\)

   Area of shaded sector:

   \(\Rightarrow \dfrac{\theta}{360^\circ} \times \pi r^2\)

   \(\Rightarrow \dfrac{72^\circ}{360^\circ} \times \dfrac{22}{7} \times (14)^2\)

   \(\Rightarrow \dfrac{72^\circ}{360^\circ} \times \dfrac{22}{7} \times 14 \times 14\)

   \(\Rightarrow \dfrac{1}{5} \times 22 \times 2 \times 14\)

   \(\Rightarrow \dfrac{616}{5}\)

   \(\Rightarrow 123.2 \ cm^2\)

   \(\therefore\) the area of the shaded sector is 123.2 cm\(^2\)

   
   
   

   ---

   
   
   
   
   
   

---

Question 4

1. Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular axes, \(Ox\) and \(Oy\) on a graph sheet.

2. On the sane graph sheet, mark the \(x-\)axis from \(-5\) to \(5\) and the \(y-\)axis from \(-6\) to \(6\).

3. \((i)\) Plot on the same graph sheet the points \(A(1, 1\frac{1}{2})\), \(B(4, 1\frac{1}{2})\), \(C(1, 4)\).

   \((ii)\) Join the points to form a triangle. What type of triangle have you drawn?

4. Draw the image \(A_1B_1C_1\) of \(ABC\) under a reflection in the \(y-\)axis where \(A \rightarrow A_1\), \(B \rightarrow B_1\) and \(C \rightarrow C_1\). Label the vertices and coordinates clearly.

5. Draw the image \(A_2B_2C_2\) of \(ABC\) under an enlargement with scale factor \(-1\) with the center of the enlargement as the origin \(0, 0\) where \(A \rightarrow A_2\), \(B \rightarrow B_2\) and \(C \rightarrow C_2\). Show the lines of enlargement and lavel the vertices and coordinates clearly.

6. What single transformation maps \(A_1B_1C_1\) onto \(A_2B_2C_2\), where \(A_1 \rightarrow A_2\), \(B_1 \rightarrow B_2\) and \(C_1 \rightarrow C_2\)

Show Solution

Solution





---

---

Question 5

1. The data below show the distribution of the ages of workers in a factory.

   

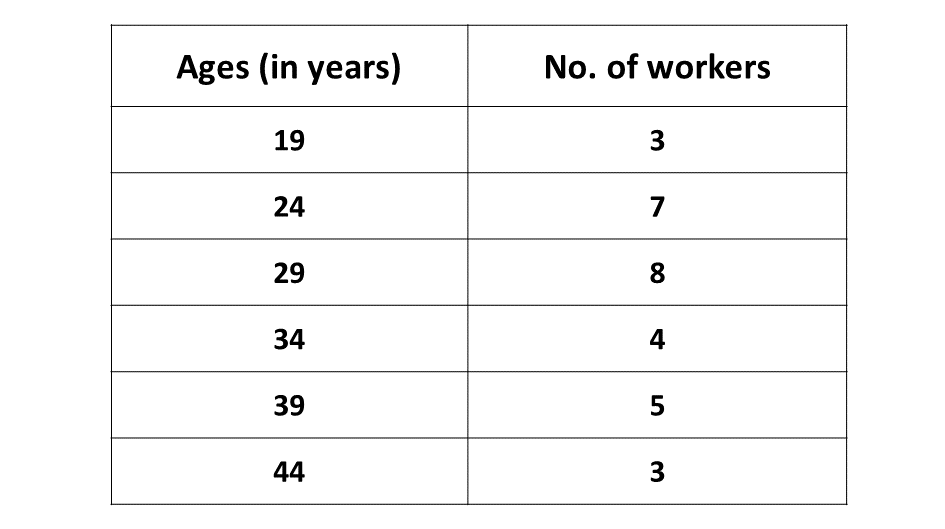
   \((i)\) How many workers are there in the factory?

   \((ii)\) What is the modal age of the distribution?

   \((iii)\) Calculate the mean age of the workers, correct to one decimal place.

Show Solution

Solution





---








2. \((i)\) Make \(T\) the subject of the relation \(I = \frac{P \times R \times T}{100}\)

   \((ii)\) If \(I = ₵40,000.00, P = ₵64,000.00\) and \(R = 25\%\), find the value of \(T\) in years.

Show Solution

Question 5b.\(i\)

\(I = \dfrac{P \times R \times T}{100}\)

Making \(T\) the subject:

\(\Rightarrow I \times 100 = \frac{P \times R \times T}{100} \times 100\)

\(\Rightarrow 100I = P \times R \times T\)

\(\Rightarrow \dfrac{100I}{P \times R} = \dfrac{P \times R \times T}{P \times R} \)

\(\Rightarrow T = \dfrac{100I}{P \times R}\)





---





Question 5b.\(ii\)

\(I = ₵40,000.00\)

\(P = ₵64,000.00\)

\(R = 25\%\)

\(T = \dfrac{100I}{P \times R}\)

\(\Rightarrow T = \dfrac{100 \times ₵40,000.00}{₵64,000.00 \times 25}\)

\(\Rightarrow T = \dfrac{100 \times ₵40}{₵64 \times 25}\)

\(\Rightarrow T = \dfrac{4 \times ₵40}{₵64}\)

\(\Rightarrow T = \dfrac{4 \times ₵5}{₵8}\)

\(\Rightarrow T = \dfrac{5}{2}\)

\(\Rightarrow T = 2\frac{1}{2}\)

\(\therefore\) time \(T\) is \(2\frac{1}{2}\) years.





---

---