PAST QUESTIONS 1997

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Take the test

---

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

---

Question 1

1. If \(p = 7, a = 16, b = -5\) and \(c = 3\),
   evaluate \(p^2 - \frac{(a - b)}{c}\)

Show Solution

Question 1a

If \(p = 7\)
\(a = 16\)
\(b = -5\)
\(c = 3\)

then \(p^2 - \dfrac{(a - b)}{c}\)

\(\Rightarrow\) \(7^2 - \dfrac{(16 - (-5))}{3}\)

\(\Rightarrow\) \(49 - \dfrac{(16 + 5)}{3}\)

\(\Rightarrow\) \(49 - \dfrac{(21)}{3}\)

\(\Rightarrow\) \(49 - 7\)

\(\Rightarrow\) \(42\)

\(\therefore\) \(p^2 - \frac{(a - b)}{c}\) is 42





---








2. Solve the inequality \(5x - 3(x - 1) \geq 39\).
   Illustrate your answer on the number line.

Show Solution

Question 1b

\(5x - 3(x - 1) \geq 39\)

\(\Rightarrow 5x - 3x + 3 \geq 39\)

\(\Rightarrow 5x - 3x \geq 39 - 3\)

\(\Rightarrow 2x \geq 36\)

\(\Rightarrow \dfrac{2x}{2} \geq \dfrac{36}{2}\)

\(\Rightarrow x \geq 18\)

\(\therefore \underline{\{x:x \geq 18\}}\)







---








3. If \(\mathbf{x} = \begin{pmatrix}-3 \\ 2 \end{pmatrix}\) and \(\mathbf{y} = \begin{pmatrix}4 \\ -1 \end{pmatrix}\), find
   \((i)\) \(\mathbf{x} + 2\mathbf{y}\)
   \((ii)\) \(3\mathbf{x} - \mathbf{y}\)

Show Solution

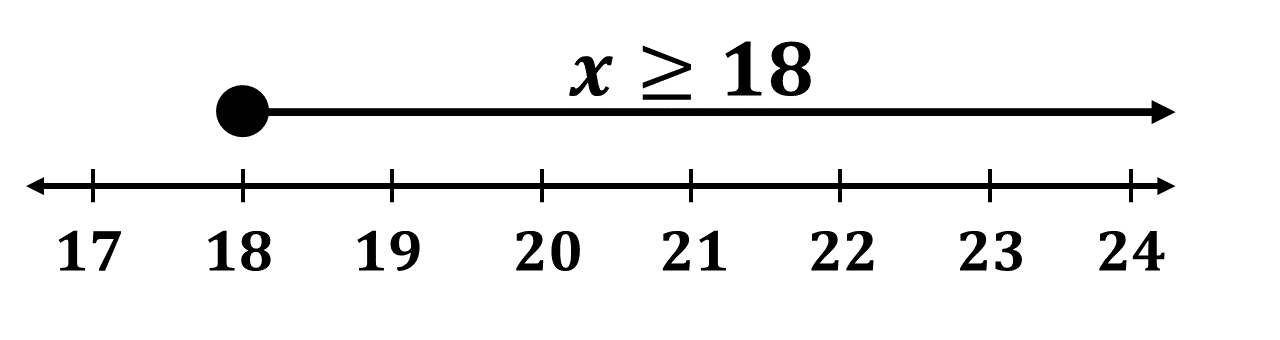
Question 1.c.

\(\mathbf{x} = \begin{pmatrix}-3 \\ 2 \end{pmatrix}\)

\(\mathbf{y} = \begin{pmatrix}4 \\ -1 \end{pmatrix}\)

1.c.i.

\(\mathbf{x} + 2\mathbf{y}\)

\(\Rightarrow\) \(\begin{pmatrix}-3 \\ 2 \end{pmatrix} + 2\begin{pmatrix}4 \\ -1 \end{pmatrix}\)

\(\Rightarrow \begin{pmatrix}-3 + 2(4) \\ 2 + 2(-1) \end{pmatrix}\)

\(\Rightarrow \begin{pmatrix}-3 + 8 \\ 2 - 2 \end{pmatrix}\)

\(\Rightarrow \begin{pmatrix} 5 \\ 0 \end{pmatrix}\)

\(\therefore \underline{\mathbf{x} + 2\mathbf{y} \ \text{is} \begin{pmatrix} 5 \\ 0 \end{pmatrix} }\)





1.c.ii.

\(3\mathbf{x} - \mathbf{y}\)

\(\Rightarrow 3\begin{pmatrix}-3 \\ 2 \end{pmatrix} - \begin{pmatrix}4 \\ -1 \end{pmatrix}\)

\(\Rightarrow \begin{pmatrix}3(-3) - 4 \\ 3(2) - (-1) \end{pmatrix} \)

\(\Rightarrow \begin{pmatrix}-9 - 4 \\ 6 + 1 \end{pmatrix} \)

\(\Rightarrow \begin{pmatrix} -13 \\ 7 \end{pmatrix} \)

\(\therefore \underline{3\mathbf{x} - \mathbf{y} \ \text{is} \begin{pmatrix} -13 \\ 7 \end{pmatrix} }\)





---

---

Question 2

1. Using a ruler and pair of compasses only:

   \((i)\) Construct triangle \(ABC\) such that \(|AB| = 8\) cm, \(|BC| = 8\) cm and \(\angle BAC = 60^\circ\).

   \((ii)\) What type of triangle is triangle \(ABC\)?

2. Contruct the bisector of \(\angle BAC\) to meet \(BC\) at \(D\). Measure \(AD\).

3. Construct the perperdicular bisector of \(AB\) to meet \(AD\) at \(O\).

4. Using \(O\) as centre and radius \(OD\), draw a circle to touch the three sides of the triangle.

Show Solution

Solution





---

---

Question 3

1. \(2y - 5x + 10 = 0, \) find

   \((i)\) \(y\), when \(x = 2\)

   \((ii)\) \(x\), when \(y = 5\)

Show Solution

Solution





---








2. Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular lines \(Ox\) and \(Oy\) on a graph sheet.

   \((i)\) On the same graph sheet mark the \(x-\)axis from \(-5\) to \(5\) and the \(y-\)axis from \(-6\) to \(6\).

   \((ii)\) Plot on the same graph sheet the points \(A(0, -5)\) and \(B(4, 5)\). Join \(AB\) using a ruler.

   \((iii)\) Find the gradient of the line \(AB\).

   \((iv)\) Measure the acute angle the line \(AB\) makes with the \(x-\)axis, using a protractor.

Show Solution

Solution





---

---

Question 4

1. The table below shows the distribution of the ages of children who were treated in a clinic in a day.

   

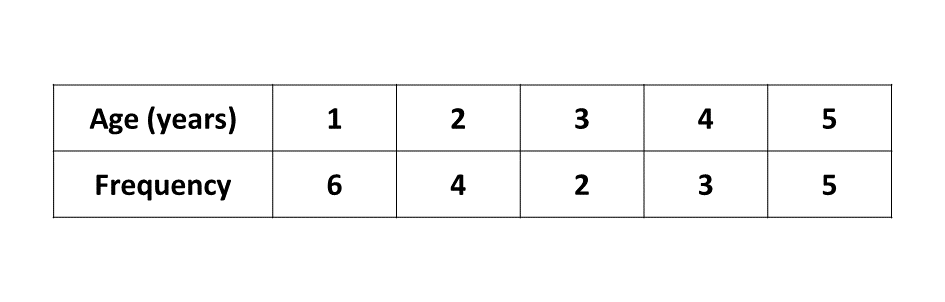
   Find

   \((i)\) the mean age,

   \((ii)\) the modal age.

2. Draw a bar chart for the distribution.

Show Solution

Solution





---

---

Question 5

1. The volume of a cylinder is \(220\) cm\(^3\), the radius of the cross section is 2.5 cm. Find the height of the cylinder. [Take \(\pi = \frac{22}{7}\)]

Show Solution

Solution





---








2. Each of the interior angles of a regular polygon is \(140^\circ\). How many sides has it?

Show Solution

Solution





---

---