PASSCO BECE 2008

PAST QUESTIONS 2008

Section A

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Section B

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

\(E\) and \(F\) are subsets of the universal set \(\mu\) such that
\(\mu = \) {natural numbers less than 15},
\(E = \) {even numbers between 1 and 15} and
\(F = \) {multiples of 4 between 9 and 15}

\((i)\) List the elements of \(\mu\), \(E\) and \(F\)

\((ii)\) Draw a Venn diagram to show the sets \(\mu\), \(E\) and \(F\)
In a school, \(\frac{7}{10}\) of the pupils like Mathematics. Half of those pupils who like Mathematics are girls. If there are 240 pupils altogether in the school, how many girls like Mathematics?
A typist charges 28 Gp for the first five sheets and 8 Gp for each additional sheet she types. How much will she earn, if she types 36 sheets?

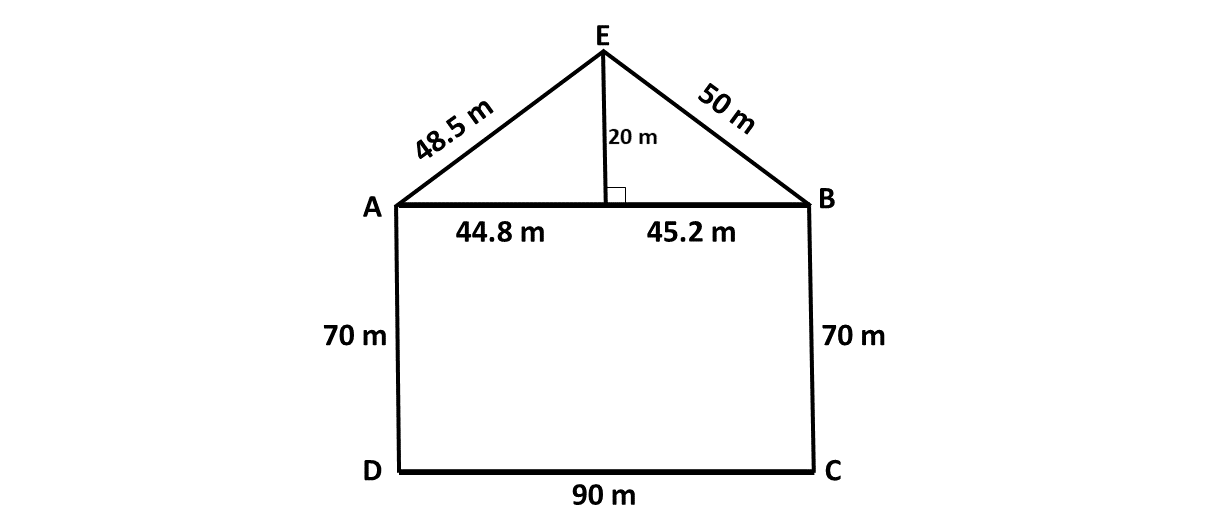
The diagram \(AEBCD\) show the shape of Mr. Awuah's garden, which is made up of a rectangular portion \(ABCD\) and a triangular portion \(AEB\).

\(|AB| = |DC| = 90\) m, \(|AD| = |BC| = 70\) m, \(|AE| = 48.5\) m and \(|EB| = 50\) m. The height of the triangle is \(20\) m.

Find

\((i)\) area of \(ABCD\),

\((ii)\) area of \(AEB\),

\((iii)\) total area of the garden,

\((iv)\) perimeter of the garden.
Find the value of \(x\) if \(\frac{3x - 2}{5}\) is greater than \(\frac{1 - 4x}{10}\) by \(5\).

A trafic survey gave the results shown in the table below:

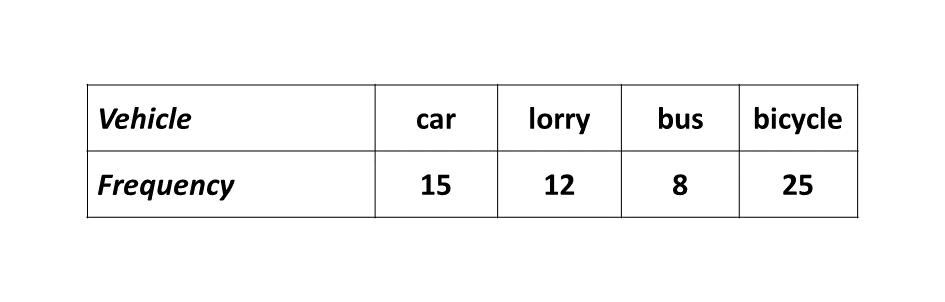
\((i)\) Represent the information on a pie chart.

\((ii)\) What percentage of the vehicles were lorries?
Akosua was granted a loan of GH₵96.00. The interest rate was 24% per annum. Calculate the

\((i)\) interest at the end of the year.

\((ii)\) total amount she had to pay at the end of the year.

\((iii)\) amount she still owes, if Akosua was able to pay only Gh₵60.00 at the end of the year.

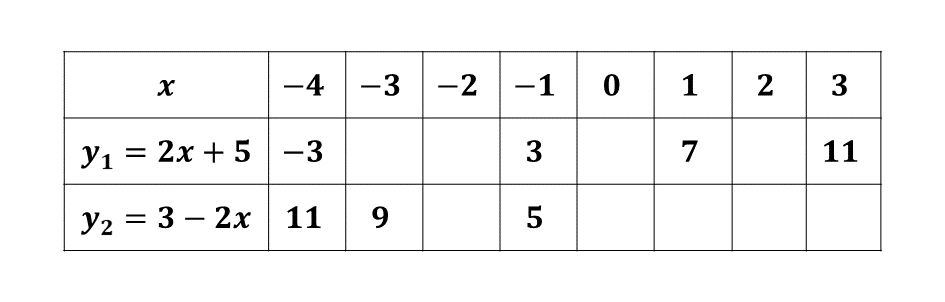
Copy and complete the table of values for the relations \(y_1 = 2x + 5\) and \(y_2 = 3 - 2x\) for \(x\) from \(-4\) to \(3\)
\((i)\) Using a scale of 2 cm to 1 unit on the \(x\)-axis and 2 cm to 2 units on the \(y\)-axis, draw two perpendicular axes \(OX\) and \(OY\) on a graph sheet.

\((ii)\) On the same graph sheet draw the graphs of the relations \(y_1 = 2x + 5\) and \(y_2 = 3 - 2x\)
Find the coordinates of the point where \(y_1\) and \(y_2\) meet.
The vectors \(\mathbf{p} = \begin{pmatrix}2 \\ 3 \end{pmatrix}\), \(\mathbf{q} = \begin{pmatrix}2 \\ 5 \end{pmatrix}\) and \(\mathbf{r} = \frac{1}{2}(\mathbf{q} + \mathbf{p})\). Find the vector \(\mathbf{r}\).

Using a ruler and a pair of compasses only,

\((i)\) construct triangle \(ABC\) with sides \(|AB| = 7\) cm, \(|BC| = 8\) cm and \(|AC| = 9\) cm;

\((ii)\) draw the perpendicular bisectors of the three sides;

\((iii)\) locate the point of intersection, \(O\), of the perpendicular bisector.

\((iv)\) with center \(O\) and radius \(OA\), draw a circle to pass through the vertices of the triangle.
Measure and write down the radius of the circle you have drawn in \((a)\) \((iv)\).
Find the product of \((2x - 3)\) and \((x - 1)\).

For sponsorship or advertisement kindly call or whatsapp on 0208711375 or 0249969740.

SHS JHS PRI 4 - 6 PASSCO

Select your level: