PAST QUESTIONS 2022

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Kindly contact the administrator of the site on WhatsApp or Phone (0208711375) for the link to the test.

---

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

---

Question 1

1. Given that \(P =\) {factors of 36} and \(Q =\) {factors of 54},

   \((i)\) List the members in the sets \(P\) and \(Q\).

   \((ii)\) Find:

   \(\hspace{0.5cm}\) A. \(P \cap Q\)

   \(\hspace{0.5cm}\) B. \(n(P \cap Q)\)

   \(\hspace{0.5cm}\) Γ. The Highest Common Factor (HCF) of 36 and 54.


Show Solution

Solution

Question 1 \((i)\)

\(P =\) {factors of 36}

\(\Rightarrow P =\) {1, 2, 3, 4, 6, 9, 12, 18, 36}

\(Q =\) {factors of 54}

\(\Rightarrow Q =\) {1, 2, 3, 6, 9, 18, 27, 54}





Question 1 \((ii)\)

\(\hspace{0.5cm}\) A. \(P \cap Q =\) {1, 2, 3, 6, 9, 18}

\(\hspace{0.5cm}\) B. \(n(P \cap Q) = 6\)

\(\hspace{0.5cm}\) Γ. The Highest Common Factor (HCF) of 36 and 54:

\(\hspace{0.8cm}\) Common factors of 36 and 54 \(\Rightarrow\) {1, 2, 3, 6, 9, 18}

\(\hspace{0.8cm}\) Highest common factor \(\Rightarrow 18\)

\(\hspace{0.8cm} \therefore\) the highest common factor of 36 and 54 is 18.





2. Write down the next two terms of the sequence 1, 4, 9, ..., ...


Show Solution

Solution





3. The median of the ordered set of observations 2, 3, (4\(m\)-3),(3\(m\)+1), 11 and 13 in ascending order is 6. Find the value of m.


Show Solution

Solution

---

Question 2

1. Simplify: \((\frac{1}{3} + \frac{1}{12}) \div (\frac{2}{3} - \frac{5}{8})\)


Show Solution

Solution





2. Find the product of \((2x - 3)\) and \((2x + 3)\).


Show Solution

Solution




3. 



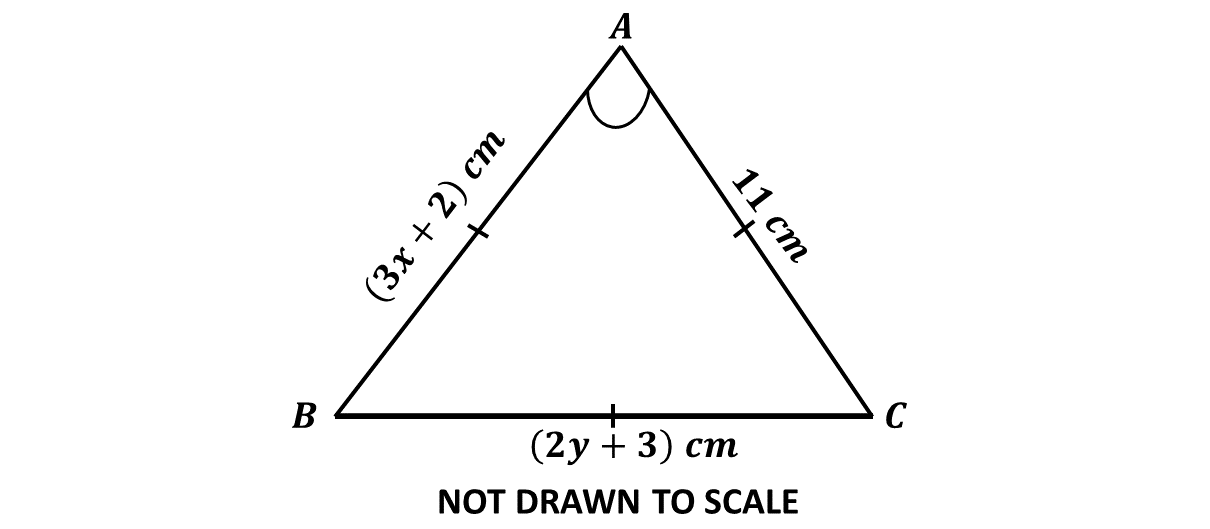
In the diagram, \(ABC\) is an equilateral triangle. Find the value of \((x + y)\).


Show Solution

Solution

---

Question 3

1. Given the relation \(L = \frac{2(m^2 - n^2)}{4(m + n)}\)

   \(\hspace{0.5cm} (i)\) simplify \(L\):

   \(\hspace{0.5cm} (ii)\) find the value of \(L\) when \(m = 2\) and \(n = 3\).


Show Solution

Solution





2. Solve \(\frac{4}{3x} = 7 - \frac{3}{x}\)


Show Solution

Solution





3. A salesman gets a commission of \(5\frac{1}{2}\%\) of the value of items he sells. The salesman sells 12 textbooks at GH₵ 25.00 per book, 3 scientific calculators at GH₵ 50.00 per calculator and 8 packets of bic pens at GH₵ 50.00 per packet. Calculate the salesman's commission.


Show Solution

Solution

---

Question 4

1. Fred is \((x - 1)\) years old now. How old:

   \(\hspace{0.5cm} (i)\) was he 4 years ago?

   \(\hspace{0.5cm} (ii)\) will he be 8 years from now?

   \(\hspace{0.5cm} (iii)\) is he now, if his age in 8 years time will be three times his age 4 years ago?


Show Solution

Solution





2. The perimeter of a rectangular cocoa farm is 497 km. The length of the farm is \(2\frac{1}{2}\) times the width. Find the:

   \(\hspace{0.5cm} (i)\) width;

   \(\hspace{0.5cm} (ii)\) length of the farm.


Show Solution

Solution

---

Question 5

1. Factorize: \((x-y)(3m+n)-(x-y)(m-2n)\)


Show Solution

Solution





2. Given that \(\mathbf{p} = \begin{pmatrix} 2 - 3x\\5 - 2y \end{pmatrix}, \ \mathbf{q} = \begin{pmatrix} -1\\5 \end{pmatrix}\) and \(\mathbf{p} - \mathbf{q} = \begin{pmatrix} 6\\8 \end{pmatrix}\).

   Find the value of \((x + y)\).


Show Solution

Solution





3. \(\hspace{0.5cm} (i)\) Find the truth set of \(\frac{x - 1}{2} \leq \frac{1}{2} + x\)

   \(\hspace{0.5cm} (ii)\) Illustrate the answer in \((i)\) on the number line.


Show Solution

Solution

---

Question 6

1. Copy and complete the table for the relation \(y = 5 - 2x\) for \(-3 \leq x \leq 4\)

   

Show Solution

Solution





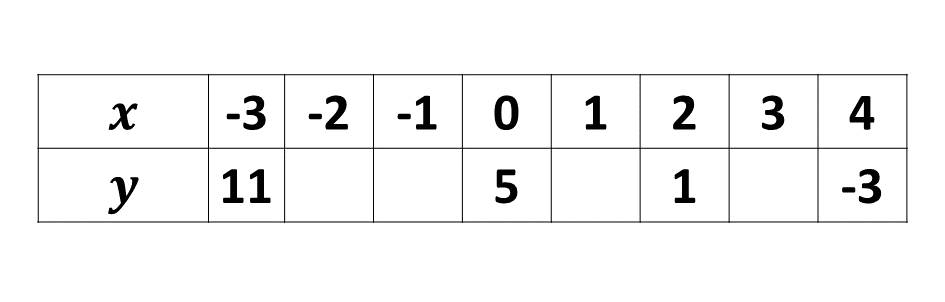
2. Using a scale of 2 cm to 1 unit on the \(x\) - axis and 2 cm to 2 units on the \(y\) - axis, draw on a graph sheet two perpendicular axes \(Ox\) and \(Oy\) for \(-5 \leq x \leq 5\) and \(-12 \leq y \leq 12\).


Show Solution

Solution





3. \(\hspace{0.5cm} (i)\) Using the table, plot all the points of the relation \(y = 5 - 2x\).

   \(\hspace{0.5cm} (ii)\) Draw a straight line through all the points.


Show Solution

Solution





4. Using the graph, find the:

   \(\hspace{0.5cm} (i)\) value of \(y\) when \(x = -2.6\);

   \(\hspace{0.5cm} (ii)\) value of \(x\) when \(y = -2.8\);

   \(\hspace{0.5cm} (iii)\) gradient of the line.


Show Solution

Solution

---