BECE
Year to Practice:
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002A
2002B
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
2015
2016
2017
2018
2019
2020
2021
2022
2023
2024
PAST QUESTIONS 1990
Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.
Click on the link below when you are ready.
Highest score: \(\mathbf{\frac{35}{40}}\)
Malvin Agyemang
Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.
Question 1
-
List the members of each of the sets
-
In a class of 60 students, 46 passed Mathematics and 42 passed English Language. Every student passed at least one of the two subjects.
\( B=\){Whole numbers from 20 to 30} and
\( D=\){factors of 63}
List the members of:
\((i)\) \(B \cap D\)
\((ii)\) \(B \cup D\)
Solution
\(B=\) {Whole numbers from 20 to 30}
\(\Rightarrow B =\) {20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30}
\(D=\) {factors of 63}
\(\Rightarrow D =\) {1, 3, 7, 9, 21, 63}
\((i)\) \(B \cap D =\) {21}
\((ii)\) \(B \cup D =\) {1, 3, 7, 9, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30}
Watch the video below for a walk-through of the solution.
\((i)\) Illustrate the information on a Venn Diagram.
\((ii)\) How many students passed in both subjects?
Let \(n\) represent the number of students who passed in both subjects.
Solution
Let \(\mathbb{U} \Rightarrow\) the total students in the class.
Let \(M \Rightarrow\) students who passed Mathematics.
Let \(E \Rightarrow\) students who passed English.
Let \(n \Rightarrow\) number of students who passed in both subjects.
\(n(\mathbb{U}) = 60\)
\(n(M) = 46\)
\(n(E) = 42\)
\((i)\)
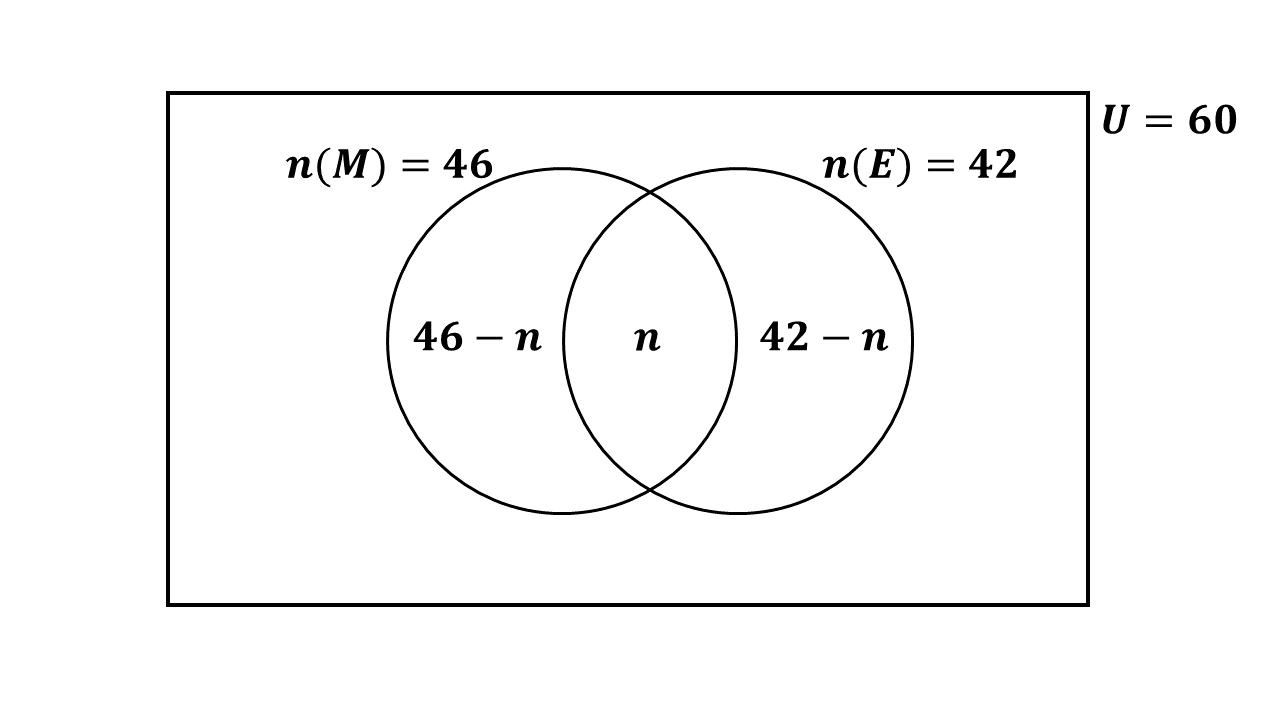
\((ii)\) \(46 -n + n + 42 - n = 60\)
\(46 + 42 - n = 60\)
\(88 - n = 60\)
\(88 - 60 = n\)
\(\Rightarrow n = 28\)
\(\therefore\) 28 students passed in both subjects.
Question 2
-
Factorise completely:
-
Solve \(\frac{x}{4} + \frac{3}{5} = \frac{3x}{2} - 2\)
-
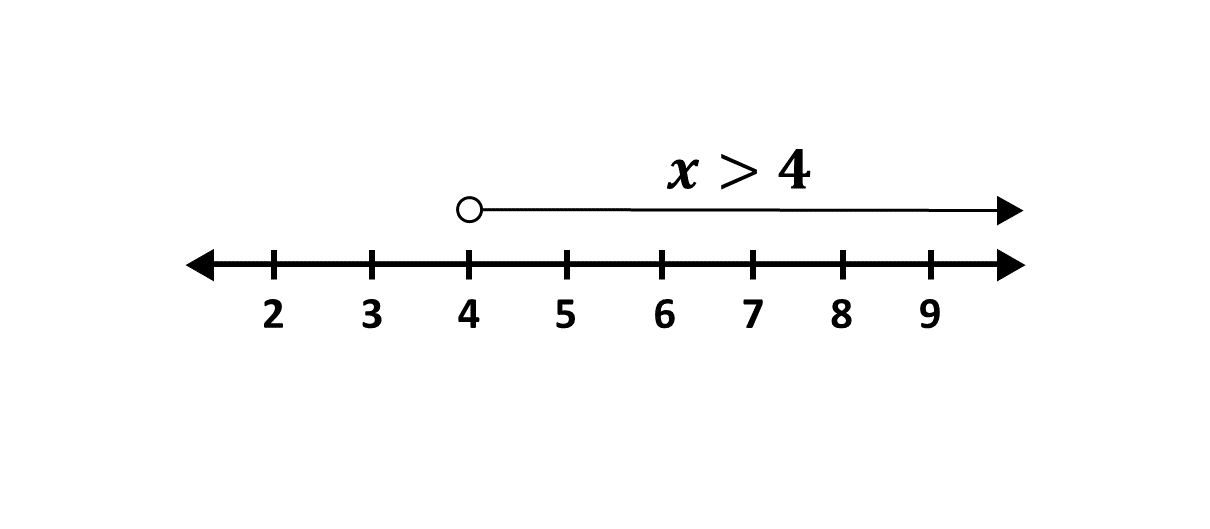
Find the solution set of \(x + 3 > 19 - 3x\), where \(x\) is a real number.
Illustrate your answer on the number line.
\(3a^2 + 2ab - 12ac - 8bc\)
Solution
\(3a^2 + 2ab - 12ac - 8bc\)
\(a(3a + 2b) - 4c(3a + 2b)\)
\(\Rightarrow (3a + 2b)(a - 4c)\)
Watch the video below for a walk-through of the solution.
Solution
\(\frac{x}{4} + \frac{3}{5} = \frac{3x}{2} - 2\)
Multiplying through by LCM of 20:
\(\Rightarrow \frac{x}{4}(20) +\) \(\frac{3}{5}(20) =\) \(\frac{3x}{2}(20) - 2(20)\)
\(\Rightarrow 5x + 3(4) = 3x(10) - 40\)
\(\Rightarrow 5x + 12 = 30x - 40\)
Grouping like terms:
\(\Rightarrow 12 + 40 = 30x - 5x\)
\(\Rightarrow 52 = 25x\)
\(\Rightarrow \frac{52}{25} = \frac{25x}{25}\)
\(\Rightarrow x = \frac{52}{25}\)
\(\Rightarrow x = 2\frac{2}{25}\)
\(\therefore x\) is \(2\frac{2}{25}\)
Watch the video below for a walk-through of the solution.
Solution
\(x + 3 > 19 - 3x\)
Grouping like-terms:
\(\Rightarrow x + 3x > 19 - 3\)
\(\Rightarrow 4x > 16\)
\(\Rightarrow \frac{4x}{4} > \frac{16}{4}\)
\(\Rightarrow x > 4\)
\(\therefore\) the solution set is {\(x:x > 4, x \in\) real numbers}
Question 3
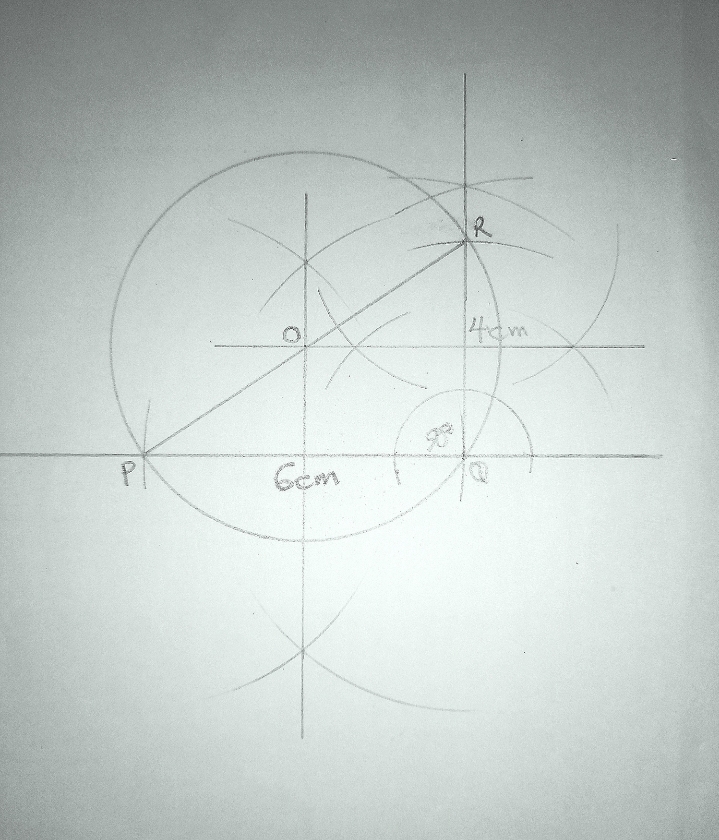
- Using a ruler and a pair of compasses only:
- Measure
\((i)\) Construct a triangle \(PQR\) such that \(|PQ| = 6cm\), \(|QR| = 4cm\) and \(\angle PQR=90°\).
\((ii)\) Construct perpendicular bisectors (mediatos) of \(PQ\) and \(QR\). Name the intersection of the mediators \(O\)
\((iii)\) Draw a circle with \(O\) as center and \(OQ\) as radius.
\((i)\) \(\lvert PR \rvert \)
\((ii)\) \(\angle QPR\)
Solution
Question 3\((a)\)
Question 3\((b)\)
\((i)\) From the diagram:
\(\hspace{0.5cm} \lvert PR \rvert = 7.2\) cm
\((ii)\) From the diagram:
\(\hspace{0.5cm} \angle QPR = 34^\circ\)
Question 4
The following is the result of a survey conducted in a class of a Junior Secondary School to find the favourite soft drink of each pupil in the class.
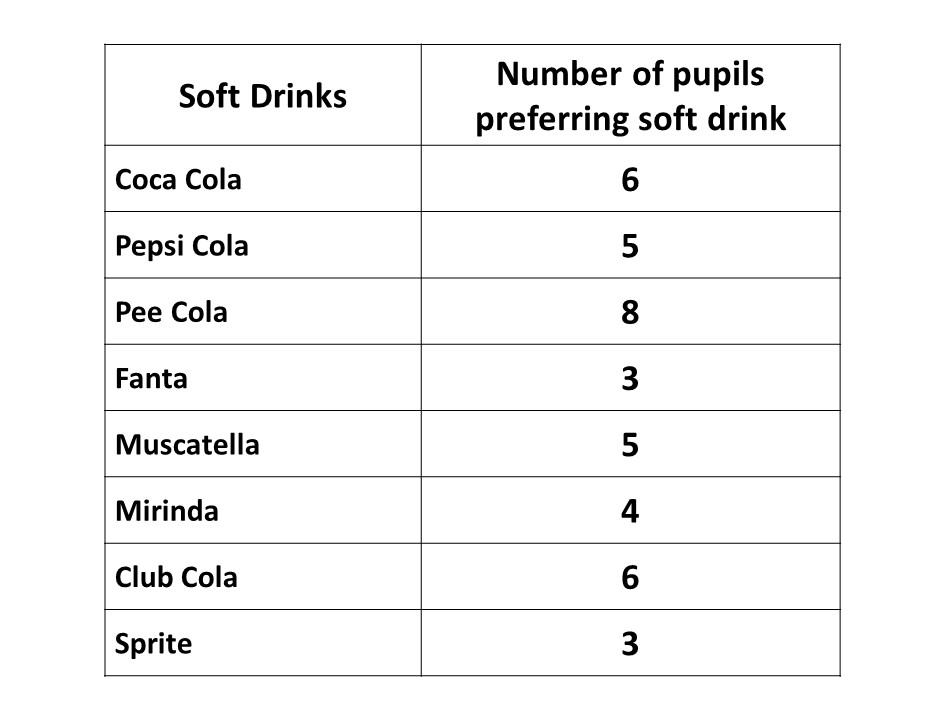
- Draw a bar chart showing this information, using a scale of 2cm to 1 unit on the vertical axis.
- How many pupils are in the class?
- What percentage of pupils in the class prefer Club Cola?
Solution
Question 4\((a)\)
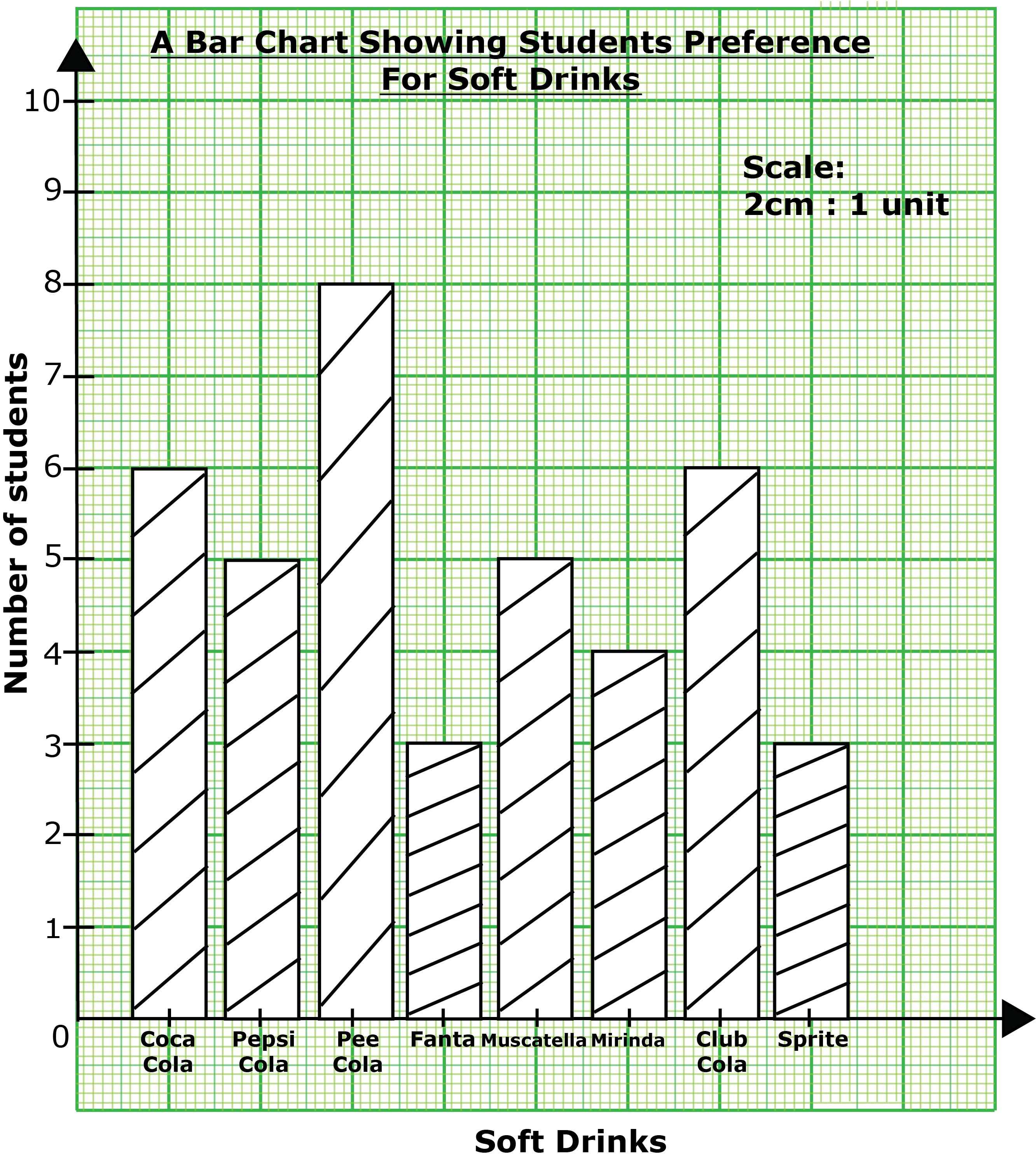
Question 4\((b)\)
Total students in the class
\(\Rightarrow \) 6 + 5 + 8 + 3 + 5 + 4 + 6 + 3
\(\Rightarrow \) 40
\(\therefore \) there are 40 students in the class.
Question 4\((c)\)
Total students in the class \( = 40\)
Number of students who prefer Club Cola \( = 6\)
Percentage of students who prefer Club Cola
\(\Rightarrow \dfrac{Number \ prefering \ Club \ Cola}{Total \ Students} \times 100\% \)
\(\Rightarrow \dfrac{6}{40} \times 100\% \)
\(\Rightarrow \dfrac{2 \times 3}{2 \times 20} \times 100\% \)
\(\Rightarrow \dfrac{3}{20} \times 100\% \)
\(\Rightarrow 3 \times 5\% \)
\(\Rightarrow 15\% \)
\(\therefore \underline{15\% \ of \ students \ prefer \ Club \ Cola.}\)
To advertise on our website kindly call on 0208711375 or 0249969740.