PAST QUESTIONS 2019

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Kindly contact the administrator of the site on WhatsApp or Phone (0208711375) for the link to the test.

---

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

---

Question 1

1. Given that \(X =\) {whole numbers from 4 to 13} and \(Y =\) {multiples of 3 between 2 and 20}, find \(X \cap Y\).


Show Solution

Solution




2. Find the Least Common Multiple (L.C.M) of the following numbers: 3, 5 and 9.

Show Solution

Solution





3. If \(\frac{p + 2q}{p} = \frac{7}{5}\), find the value of \(\frac{q}{p}\).


Show Solution

Solution

---

Question 2

1. Solve: \(\frac{4x + 5}{5} + \frac{x - 3}{4} = -1\)

Show Solution

Solution





2. The ratio of boys to girls in a school is \(12:25\). If there are \(120\) boys.

   \((i)\) how many girls are in the school?

   \((ii)\) what is the total number of boys and girls in the school?

Show Solution

Solution





3. Simplify: \((8x^2y^3)(\frac{3}{8}xy^4)\)

Show Solution

Solution

---

Question 3

1. In an examination, 60 candidates passed Integrated Science or Mathematics. If 15 passed both subjects and 9 more passed Mathematics than Integrated Science, find the:

   \((i)\) number of candidates who passed in each subject;

   \((ii)\) probability that a candidate passed exactly one subject.

Show Solution

Solution





2. Factorize: \(xy + 6x + 3y + 18\)

Show Solution

Solution

---

Question 4

1. Express 250% as a fraction in its lowest term.

Show Solution

Solution




2. 

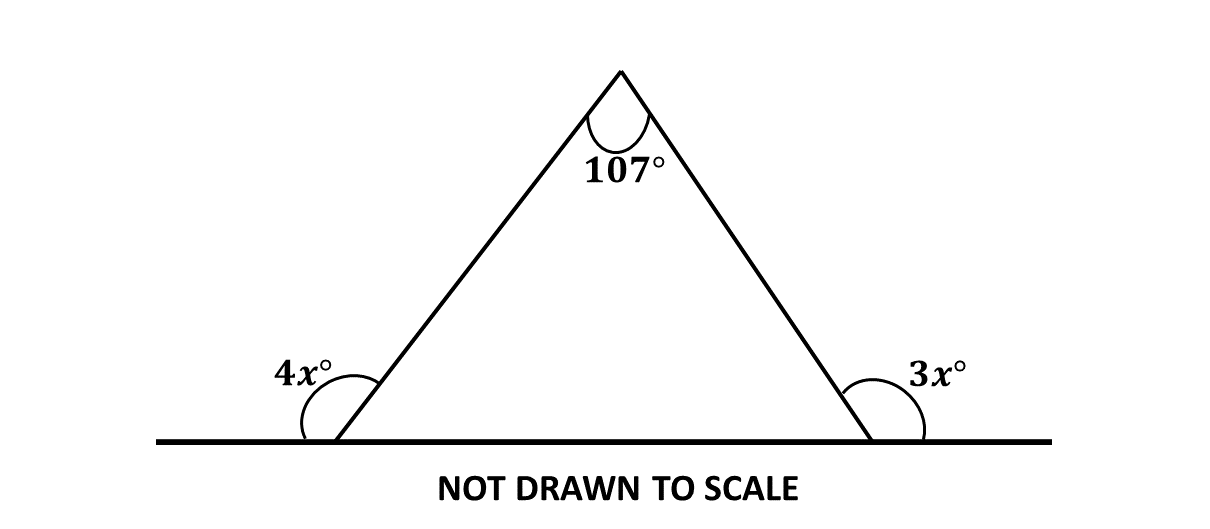
   Use the diagram to find the value of \(x\).

Show Solution

Solution





3. Simplify: \(2 \div (\frac{15}{64} \div \frac{6}{7})\)

Show Solution

Solution





4. If \(\mathbf{q = \begin{pmatrix} 7\\ -1 \end{pmatrix}}\) and \(\mathbf{r = \begin{pmatrix} 4\\ -5 \end{pmatrix}}\), find \((\mathbf{q} + \mathbf{r})\).

Show Solution

Solution

---

Question 5

1. 

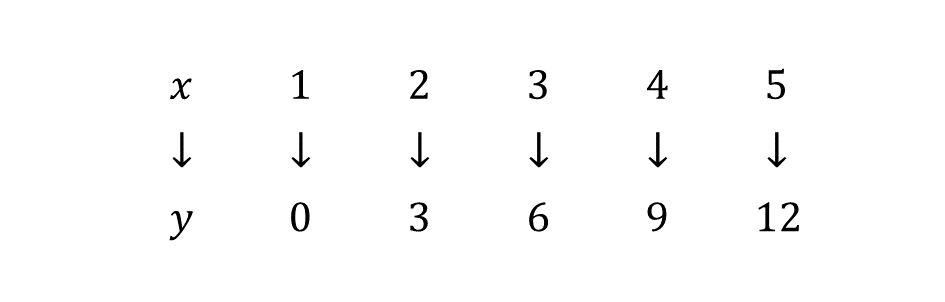
   The mapping shows the relationship between \(x\) and \(y\).

   \((i)\) Using a scale of 2 cm to 1 unit on the \(x\) - axis and 2 cm to 2 units on the \(y\) - axis, draw two perpendicular axes \(Ox\) and \(Oy\) on a graph sheet for \(1 \leq x \leq 5\) and \(0 \leq x \leq 14\);

   \((ii)\) Plot the point for each ordered pair, \((x, y)\).

   \((iii)\) Join the points with a straight line;

   \((iv)\) Using the graph sheet, find the gradient of the line in \((a)(iii)\).

   \((v)\) Use the graph to find the equation of the line in \((a)(iii)\).

Show Solution

Solution





2. Simplify: \(32 \times 8 \times 4 \times 2\), leaving your answer in the form \(2^n\).

Show Solution

Solution

---

Question 6

The marks obtained by students in a class test were:

\(\hspace{0.5cm} 4 \hspace{0.5cm} 8 \hspace{0.5cm} 7 \hspace{0.5cm} 6 \hspace{0.5cm} 7\)
\(\hspace{0.5cm} 2 \hspace{0.5cm} 1 \hspace{0.5cm} 7 \hspace{0.5cm} 4 \hspace{0.5cm} 7\)
\(\hspace{0.5cm} 3 \hspace{0.5cm} 7 \hspace{0.5cm} 6 \hspace{0.5cm} 4 \hspace{0.5cm} 3\)
\(\hspace{0.5cm} 7 \hspace{0.5cm} 5 \hspace{0.5cm} 2 \hspace{0.5cm} 7 \hspace{0.5cm} 2\)
\(\hspace{0.5cm} 5 \hspace{0.5cm} 4 \hspace{0.5cm} 8 \hspace{0.5cm} 3 \hspace{0.5cm} 2\)

1. Construct a frequency distribution table for the data.

Show Solution

Solution





2. Find the:

   \((i)\) mode of the distribution.

   \((ii)\) median mark of the test.

   \((iii)\) mean mark.

Show Solution

Solution

---