PAST QUESTIONS 1991

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Take the test

Highest score: \(\mathbf{\frac{28}{40}}\)

Queenster Obeng

---

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

---

Question 1

1. If \(X=\) {Prime numbers less than 13} and \(Y=\) {odd numbers less than 13}

\((i)\) List the members of \(X\) and \(Y\).

\((ii)\) List the members of \(X \cap Y\) and \(X \cup Y\)


Show Solution

Solution

Question \((1.a.i.)\)

\(X = \){Prime numbers less than 13}

\(\therefore \ X = \{2, 3, 5, 7, 11\}\)

\(Y = \){Odd numbers less than 13}

\(\therefore \ Y = \{1, 3, 5, 7, 9, 11\}\)




Question \((1.a.ii.)\)

\(X = \{2, 3, 5, 7, 11\}\)

\(Y = \{1, 3, 5, 7, 9, 11\}\)

\(\Rightarrow X \cap Y = \{3, 5, 7, 11\} \)

\(\Rightarrow X \cup Y = \{1, 2, 3, 5, 7, 9, 11\} \)

\(\therefore X \cap Y = \{3, 5, 7, 11\}\) and \(X \cup Y = \{1, 2, 3, 5, 7, 9, 11\}\)





---












2. Three school children share some oranges as follows:

   Akwasi gets \(\frac{1}{3}\) of the total, and the remainder is shared between Abena and Jantuah in the ratio \(3 : 2\). If Jantuah gets 24 oranges, how many does Akwasi get?

Show Solution

---

Question 2

Using a ruler and a pair of compasses only

1. Construct a triangle \(XYZ\) in which \(|YZ|=6cm\), \(\angle YZX=\) 60° and \(|ZX|= 9cm\). Measure \(|XY|\)

2. \((i)\) Construct the mediator of \(XY\)

\((ii)\) Draw a circle center \(X\) and a radius of 5 cm. Measure \(|YA|\), where \(A\) is the point of intersection of the mediator and the circle in the triangular region \(XYZ\)

Show Solution

---

Question 3

1. Solve the equation \(\dfrac{2x-1}{3} - \dfrac{x-2}{4} =1\)

   Show Solution

   Solution

   \(\dfrac{2x-1}{3} - \dfrac{x-2}{4} =1\)

   Multiplying through by an L.C.M of \(12\)

   \(\Rightarrow 12 \left(\dfrac{2x-1}{3}\right)\)\(- 12 \left(\dfrac{x-2}{4}\right)\)\(=12 (1)\)

   \(\Rightarrow 4(2x - 1)\)\(- 3(x - 2)\)\(= 12\)

   \(\Rightarrow 8x - 4\)\( - 3x + 6\)\(= 12\)

   \(\Rightarrow 8x - 3x\)\( - 4 + 6\) \(= 12\)

   \(\Rightarrow \hspace{1.2cm} 5x + 2\) \(= 12\)

   \(\Rightarrow \hspace{1.8cm} 5x = 12 - 2\)

   \(\Rightarrow \hspace{1.8cm} 5x = 10\)

   \(\Rightarrow \hspace{1.6cm} \dfrac{5x}{5} = \dfrac{10}{5} \)

   \(\Rightarrow \hspace{1.8cm} x = 2\)

   \(\therefore x\) is 2.

   
   
   

   ---

   
   
   



2. Factorise completely \(2ap+aq-bq-2bp\)

   Show Solution

   Solution

   \(2ap+aq-bq-2bp\)

   \(\Rightarrow (2ap+aq)-(bq+2bp)\)

   \(\Rightarrow a(2p+q)-b(q+2p)\)

   \(\Rightarrow a(2p+q)-b(2p+q)\)

   \(\Rightarrow (2p+q)(a-b)\)

   
   
   

   ---

   
   
   



3. Given that \(m = -2\) and \(n = \dfrac{3}{4}\), find the value of

   \((i)\) \(m^2(n-1)\)

   \((ii)\) \(n^2 - \dfrac{3}{m}\)

   Show Solution

   Solution

   \(m = -2\)

   \(n = \dfrac{3}{4}\)

   
   

   Question (3.c.\(i\))

   \(m^2(n-1)\)

   Substituting \(m\) and \(n\) into expression:

   \(\Rightarrow (-2)^2(\frac{3}{4}-1) \)

   \(\Rightarrow 4(\frac{3}{4}-1) \)

   Expanding the bracket:

   \(\Rightarrow (4 \times \frac{3}{4}) - (4 \times 1) \)

   \(\Rightarrow 3 - 4 \)

   \(\Rightarrow - 1 \)

   \(\therefore\) when m is \(-2\) and \(n\) is \(\frac{3}{4}\), \(m^2(n-1)\) is \(-1\).

   
   

   Question (3.c.\(ii\))

   \(n^2 - \dfrac{3}{m}\)

   Substituting \(m\) and \(n\) into expression:

   \(\Rightarrow (\dfrac{3}{4})^2 - \dfrac{3}{-2}\)

   \(\Rightarrow (\dfrac{3^2}{4^2}) + \dfrac{3}{2}\)

   \(\Rightarrow \dfrac{9}{16} + \dfrac{3}{2}\)

   \(\Rightarrow \dfrac{9 \ + \ 8(3)}{16}\)

   \(\Rightarrow \dfrac{9 \ + \ 24}{16}\)

   \(\Rightarrow \dfrac{33}{16}\)

   \(\Rightarrow 2\dfrac{1}{16}\)

   \(\therefore\) when m is \(-2\) and \(n\) is \(\frac{3}{4}\), \(n^2 - \frac{3}{m}\) is \(2\frac{1}{16}\).

   
   
   

   ---

   
   
   

---

Question 4

1. The following table shows the distribution of voters in an election for class prefect.




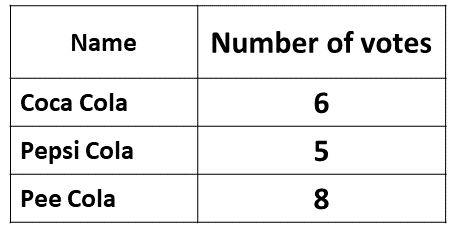
\((i)\) Draw a pie chart to illustrate the information.

\((ii)\) What fraction of the votes was cast for Borquaye?


Show Solution

Question 4.a.\((i)\)

Total number of votes

\(\Rightarrow 6 + 12 + 18\)

\(\Rightarrow 36\)

Angle of sector \(= \dfrac{frequency}{total \ frequency} \times 360^\circ\)

Angle of sector for Acquaye:

\(\Rightarrow \dfrac{6}{36} \times 360^\circ\)

\(\Rightarrow 6 \times 10^\circ\)

\(\Rightarrow 60^\circ\)

Angle of sector for Borquaye:

\(\Rightarrow \dfrac{12}{36} \times 360^\circ\)

\(\Rightarrow 12 \times 10^\circ\)

\(\Rightarrow 120^\circ\)

Angle of sector for Commey:

\(\Rightarrow \dfrac{18}{36} \times 360^\circ\)

\(\Rightarrow 18 \times 10^\circ\)

\(\Rightarrow 180^\circ\)




Pie chart showing the distribution.







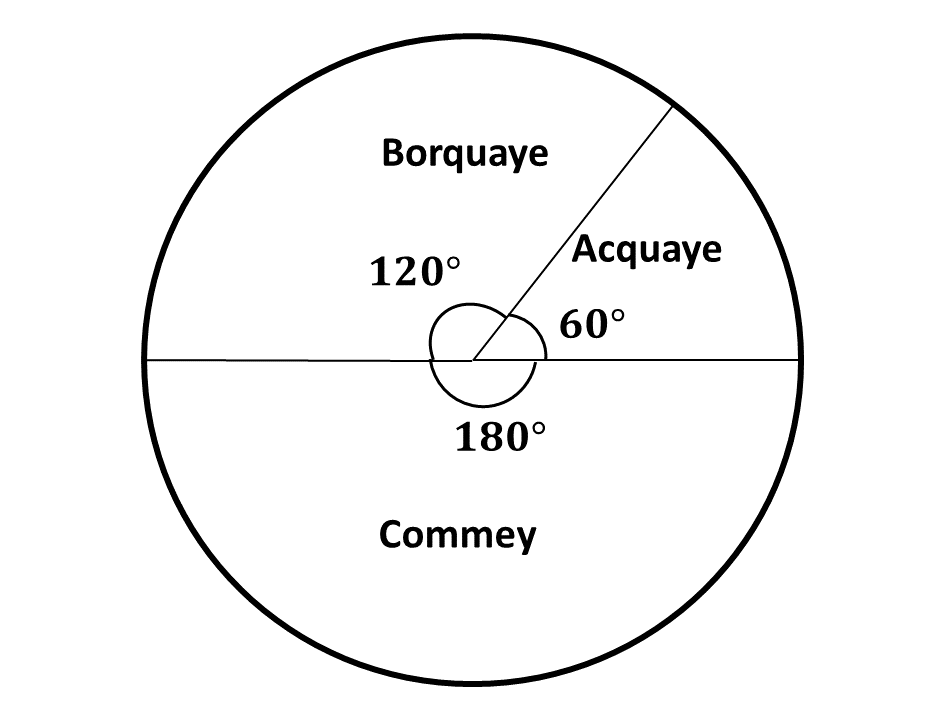
Question 4.a.\((ii)\)

Fraction of votes cast for Borquaye

\(\Rightarrow \dfrac{Borquaye's \ votes}{Total \ votes}\)

\(\Rightarrow \dfrac{12}{36}\)

\(\Rightarrow \dfrac{1 \times 12}{3 \times 12}\)

\(\Rightarrow \dfrac{1}{3}\)

\(\therefore\) fraction of votes cast for Borquaye is \(\dfrac{1}{3}\).





---








2. The height in centimeters of 10 school children are as follows:

165, 165, 155, 159, 174,
154, 169, 155, 155, 150

\((i)\) Make a frequency table for the data.

\((ii)\) Use your table to find the mode and the median of the distribution.


Show Solution

Question 4.b.\((i)\)

Frequency table for distribution.







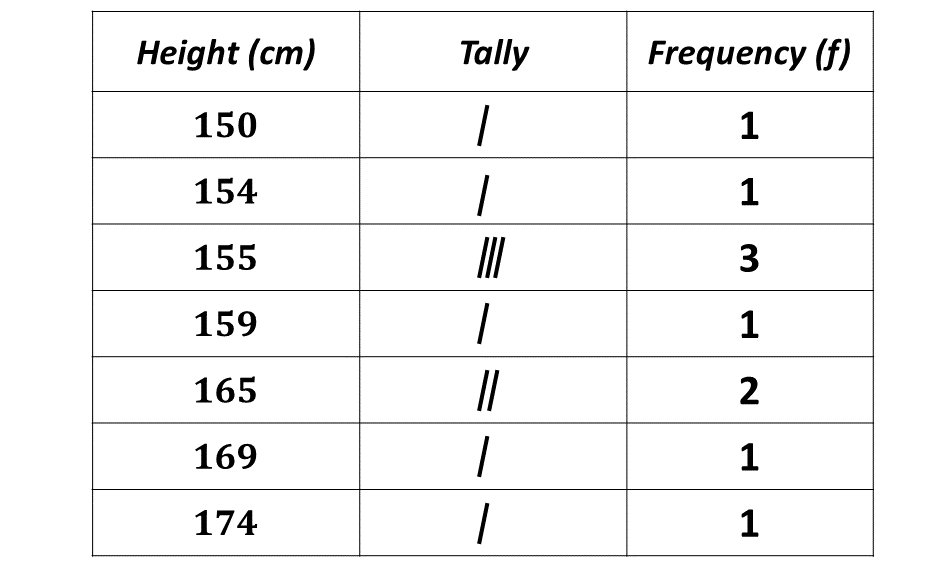
Question 4.b.\((ii)\)

Mode \(\Rightarrow\) the highest occuring number.

\(\therefore\) mode \(= 155\)

Median \(\Rightarrow\) the middle number.

median \(= \frac{155 + 159}{2}\)

median \(= 157\)

\(\therefore\) the mode and median of the distribution are 155 and 157 respectively.





---

---