PAST QUESTIONS 2000

Time yourself to improve on your speed. You are to use not more than 60 minutes for this section.

Click on the link below when you are ready.

Take the test

---

Try the questions first, using not more than 15 minutes for each question, and watch the accompanying videos to see how the questions are solved.

---

Question 1

1. Simplify \(\frac{2}{3}\) of \(6\frac{3}{4} \div (2\frac{4}{15} - 1\frac{2}{3})\)

Show Solution

Solution

\(\frac{2}{3}\) of \(6\frac{3}{4} \div (2\frac{4}{15} - 1\frac{2}{3})\)

\(\Rightarrow \frac{2}{3}\) of \(\frac{27}{4} \div \left(\frac{34}{15} - \frac{5}{3}\right)\)

\(\Rightarrow \dfrac{2}{3}\) of \(\dfrac{27}{4} \div \left(\dfrac{1(34) - 5(5)}{15}\right)\)

\(\Rightarrow \dfrac{2}{3}\) of \(\dfrac{27}{4} \div \left(\dfrac{34 - 25}{15}\right)\)

\(\Rightarrow \dfrac{2}{3}\) of \(\dfrac{27}{4} \div \dfrac{9}{15}\)

\(\Rightarrow \left(\dfrac{2}{3} \times \dfrac{27}{4}\right) \div \dfrac{9}{15}\)

\(\Rightarrow \dfrac{9}{2} \div \dfrac{9}{15}\)

\(\Rightarrow \dfrac{9}{2} \times \dfrac{15}{9}\)

\(\Rightarrow \dfrac{15}{2}\)

\(\Rightarrow \underline{\underline{7\frac{1}{2}}}\)





---












2. Solve the equation:

   \(\frac{1}{3}(x + 3) - 2(x - 5) = 4\frac{1}{3}\)

Show Solution

Solution

\(\frac{1}{3}(x + 3) - 2(x - 5) = 4\frac{1}{3}\)

\(\Rightarrow \frac{1}{3}(x + 3) - 2(x - 5) = \frac{13}{3}\)

Multiplying through by the L.C.M

\(\Rightarrow 3 \times \frac{1}{3}(x + 3) - 3(2(x - 5)) = 3 \times \frac{13}{3}\)

\(\Rightarrow (x + 3) - 3(2x - 10) = 13\)

\(\Rightarrow x + 3 - 6x + 30 = 13\)

\(\Rightarrow x - 6x = 13 - 3 - 30\)

\(\Rightarrow -5x = -20\)

\(\Rightarrow \dfrac{-5x}{-5} = \dfrac{-20}{-5}\)

\(\Rightarrow x = 4\)

\(\therefore \underline{x \ is \ 4}.\)





---












3. If \(3y = 2x^2 - 3x + 7\), find \(y\) when \(x = 5\)

Show Solution

Solution

\(3y = 2x^2 - 3x + 7\)

when \(x = 5\)

\(\Rightarrow\) \(3y = 2(5^2) - 3(5) + 7\)

\(\Rightarrow\) \(3y = 2(25) - 15 + 7\)

\(\Rightarrow\) \(3y = 50 - 15 + 7\)

\(\Rightarrow\) \(3y = 35 + 7\)

\(\Rightarrow\) \(3y = 42\)

\(\Rightarrow\) \(\dfrac{3y}{3} = \dfrac{42}{3}\)

\(\Rightarrow y = 14\)

\(\therefore\) when \(x\) is 5, \(y\) is 14.





---

---

Question 2

1. In a diagram \(PADQ\) and \(RBCS\) are parallel lines. \(|BD| = |DC|\), angles \(ABD = 65^\circ\) and angle \(ABR = 50^\circ\).

   

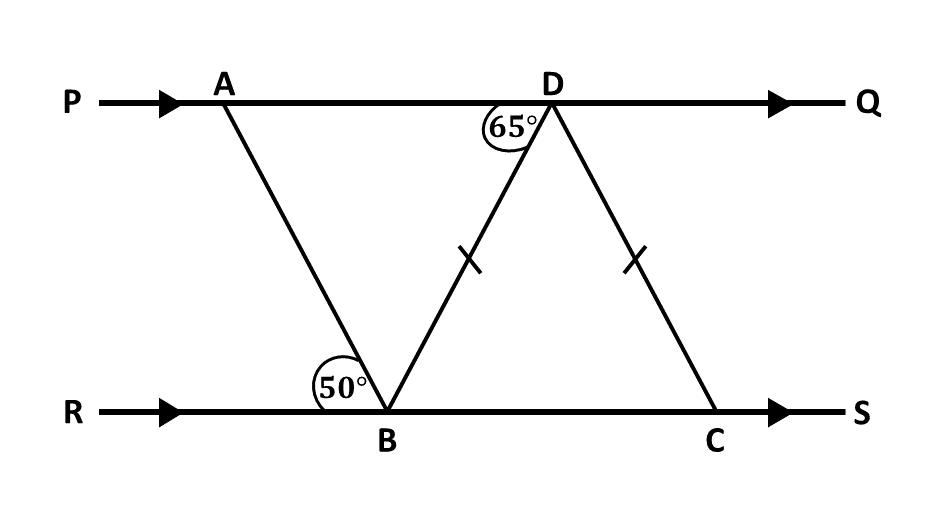
   \((i)\) Calculate angle \(BDC\).

   \((ii)\) Calculate angle \(ABD\)

   \((iii)\) Find angle \(BAD\).

   \((iv)\) What type of triangle is triangle \(ABD\)?

Show Solution

Solution





---








2. Using a ruler and a pair of compasses only, construct triangle \(XYZ\), with \(|YZ| = 8\) cm, angle \(XYZ = 60^\circ\) and \(|XY| = 9\) cm. Measure

   \((i)\) angle \(YZX\)

   \((ii)\) \(|XZ|\)

Show Solution

Solution





---

---

Question 3

Ama was granted a loan of ₵800,000.00 by a bank. The rate of interest was 42% per annum.

1. Calculate,

   \(\hspace{0.5cm} i)\) the interest at the end of the year.

   \(\hspace{0.5cm} ii)\) the total amount Ama had to pay at the end of the year.

2. Ama was able to pay only ₵700,000.00 at the end of the year.

   \((i)\) Find how much Ama still owned the bank.

   \((ii)\) Express the amount owned after paying the bank ₵700,000.00 to the bank as a percentage of the loan she took from the bank.

Show Solution

Solution





---

---

Question 4

The following is a record of scores obtained by 30 J.S.S form 2 pupils in a test marked out of 5.

\(\hspace{0.5cm} 5, 3, 2, 4, 5, 2, 4, 3, 1, 1\)
\(\hspace{0.5cm} 3, 4, 2, 3, 4, 5, 3, 4, 3, 2\)
\(\hspace{0.5cm} 4, 3, 1, 2, 2, 3, 3, 2, 4, 3\)



1. Copy and complete the table.

2. Find the mean of the distribution.

3. If a pupil is selected at random from the form, what is the probability that he\she scored 4 marks?

Show Solution

Solution





---

---

Question 5

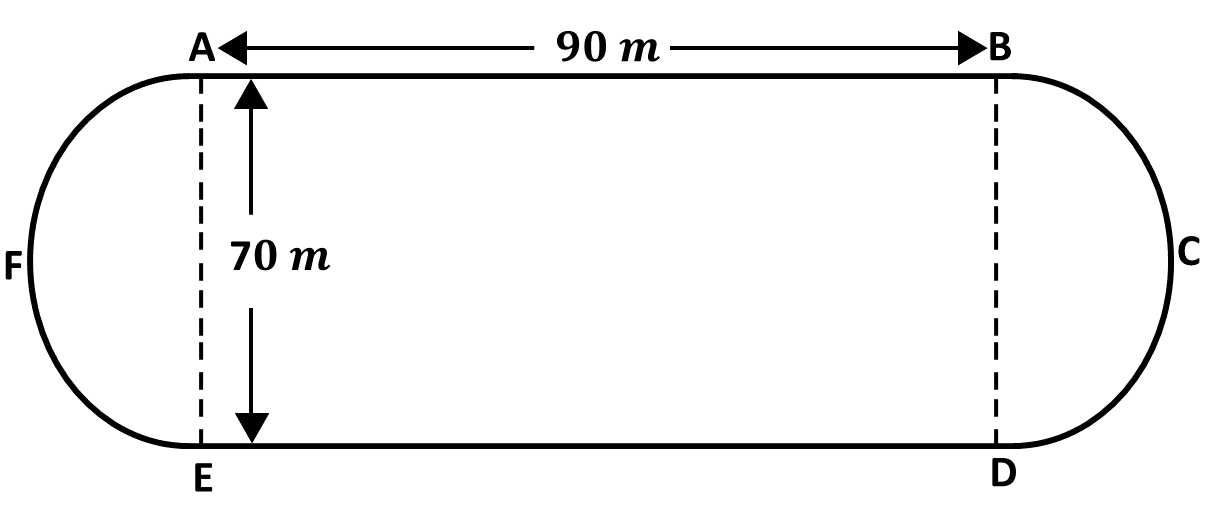
The diagram shows a running track \(ABCDEF\). \(AB\) and \(ED\) are the straight sides. The ends \(AFE\) and \(BCD\) are semi circular shapes.
\(AB = ED = 90\) m and \(AE = BD = 70\) m. Find

1. the total length of the two semi circular ends, \(AFE\) and \(BCD\).

2. the perimeter of the running track \(ABCDEFA\).

3. the total area of the running track \(ABCDEFA\). [Take \(\pi = \frac{22}{7}\)]

Show Solution

Solution





---

---