In our previous lesson, we learnt how to deduce the area of a triangle from the area of a parallelogram.
We learnt that the parallelogram is a four sided figure with opposite sides parallel and equal. If you draw a diagonal line within a parallelogram, it divides the parallelogram into two triangles of equal area.
The formular for the area of a parallelogram is given as:\[Base \times Height\].
Which can also be written as: \[Length \times Width\].
Since the two triangles created by the diagonal inside of the parallelogram have their areas being equal, we can therefore say, that the area of one triangle is half of the area of the parallelogram.
Mathematically, we write;
Area of triangle = \(\mathbf{\frac{1}{2} \times base \times height}\)
Remember, that the height is the perpendicular height of the triangle and not the slanted height.
Also, since the base can be said to be the length, and the height considered as the width, we can re-write the formula above as;
Area of triangle = \(\mathbf{\frac{1}{2} \times Length \times Width}\)
We will use the formulars above in solving questions with regards to the area of a triangle in this lesson.
Consider the examples below:
Example 1
The base of a triangle is 12 cm, and its height is 5 cm. Calculate the area.
Solution
Example 2
A triangle with a base of 10 m and a height of 7 m is given. What is its area?
Solution
Example 3
If the height of a triangle is 4 cm and its base is 9 cm, find the area.
Solution
Example 4
A triangle has an area of \(24 \ cm^2\). If its base is 6 cm, find its height.
Solution
Example 5
A triangle is formed inside a rectangle with a base of 14 cm and a height of 10 cm. If the triangle's base is the same as the rectangle's, find the area of the triangle.
Solution
Example 6
The base of a triangle is 25 cm, and its height is 14 cm. Calculate the area in square centimeters.
Solution
Example 7
The area of a triangle is \(45 m^2\). If the height is 5 m, find the length of the base.
Solution
Example 8
A parallelogram has an area of \(72 cm^2\) and is divided into two equal triangles. What is the area of one triangle?
Solution
Example 9
A right-angled triangle has legs measuring 9 cm and 12 cm. Calculate its area.
Solution
Example 10
Find the area of the triangle below:
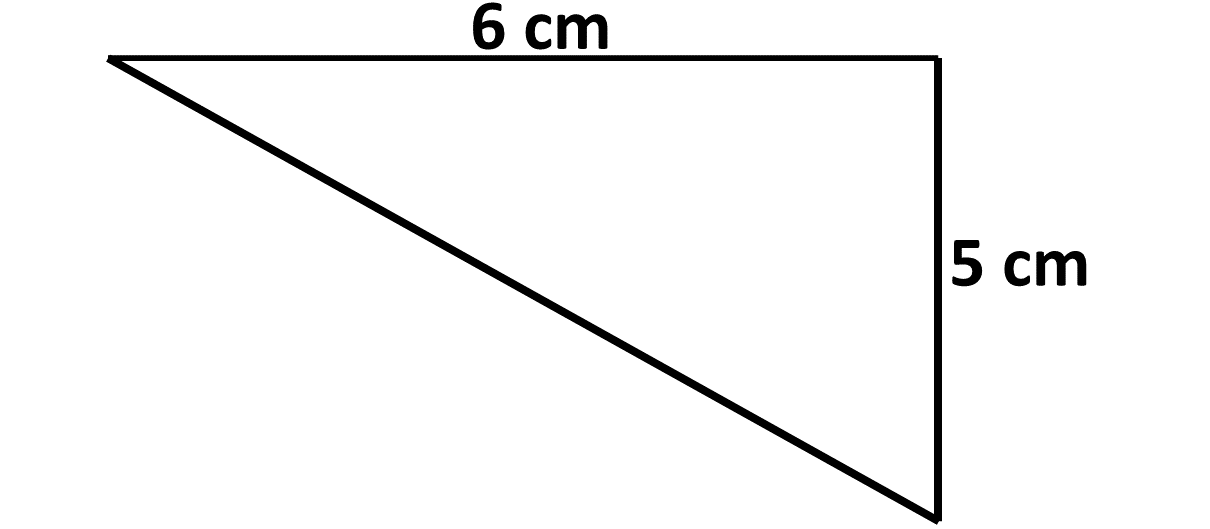
Solution
Example 11
Find the area of the triangle below:
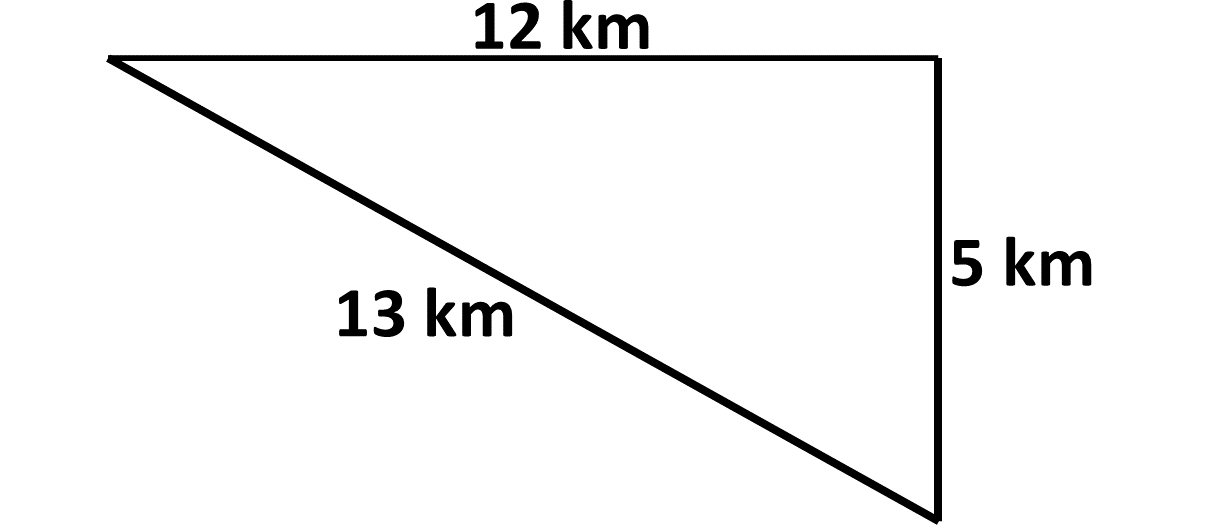
Solution
Example 12
Find the area of the triangle below:
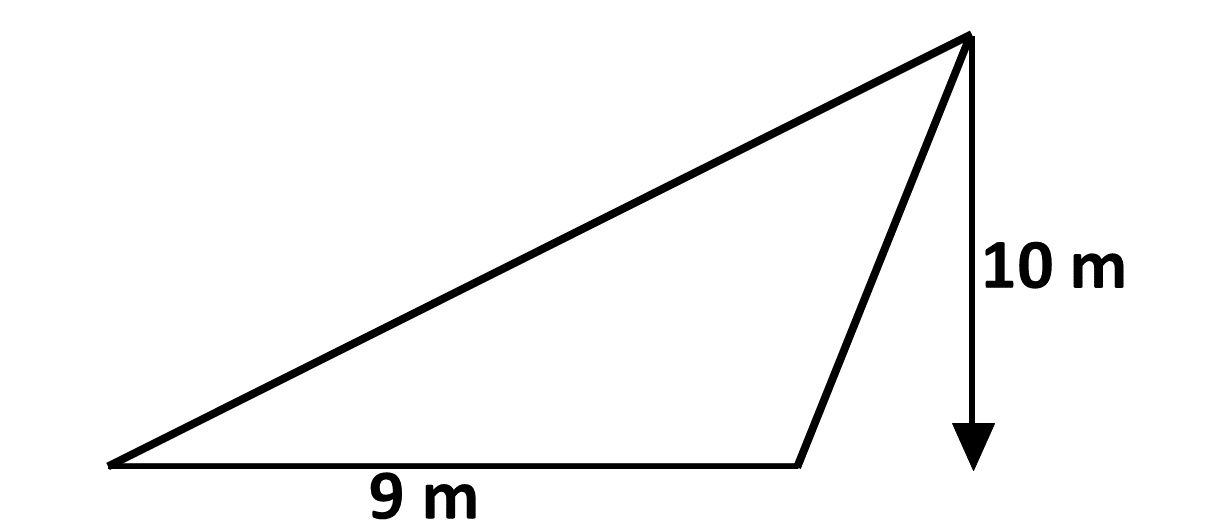
Solution
Example 13
Find the area of the triangle below:
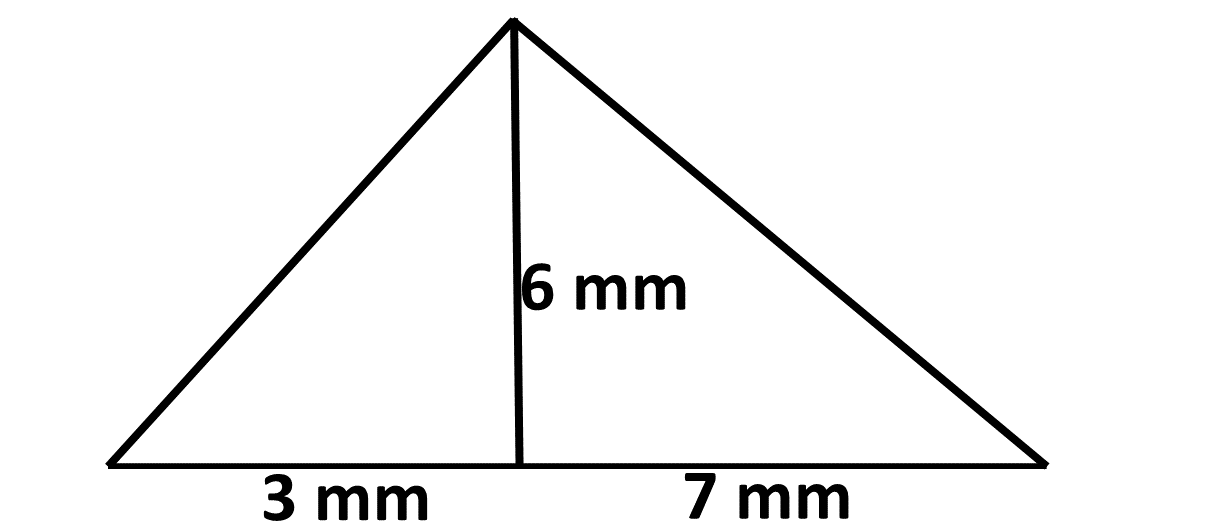
Solution
Example 14
A triangle has a base of 10 m and a height of 6 m. If both the base and height are doubled, what will be the new area of the triangle?
Solution
Example 15
The sides of a triangle are 13 cm, 14 cm, and 15 cm. Use Heron's formula to calculate its area.
Solution
Solve the following
-
A triangle's height is 1.5 times its base. If the base is 10 cm, find the area of the triangle.
-
The area of a triangle is \(50 \ cm^2\), and its height is twice its base. Find the base and height of the triangle.
-
A triangle has a base of 12 cm and an area of \(48 \ cm^2\). What is the length of its height?
-
What is the area of a triangle with a base of 15 m and a height of 8 m?
-
Calculate the area of a right-angled triangle with a base of 7 cm and a perpendicular height of 9 cm.
-
Find the base of a triangle if its area is \(36 \ cm^2\) and its height is 6 m.
-
A triangle has an area of \(24 \ cm^2\) and a base of 8 cm. What is its height?
-
What is the area of a triangle with a base of 10 cm and a height of 5 cm?
-
In a triangle, the height is 5 cm longer than the base. If the area is \(60 cm^2\), find the base and height of the triangle.
-
A triangle has sides of 6 cm, 8 cm, and 10 cm. Verify if it is a right triangle and calculate its area.
Test yourself on what you have learnt so far. Click on the link below when you are ready.
Kindly contact the administrator on 0208711375 for the link to the test.
For sponsorship or advertisement kindly call or whatsapp on 0208711375 or 0249969740.