The area of any given shape is defined as the enclosed space within the boundary of the shape. It is a very important concept in Mathematics.
In this lesson, we will use the relationship between parallelograms, to deduce the formular for the area of a triangle.
A parallelogram is a four-sided figure with opposite sides parallel and equal. Examples, of parallelograms are square, rectangle, rhombus etc.
We will use the rectangle to deduce the formular of a triangle.
A rectangle is a four-sided figure with opposite sides equal and all angles right angles. The formula for the area of a rectangle is given by: \[Area = base \times height\]
Below is a diagram of a rectangle:
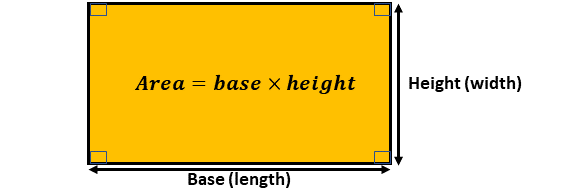
The base is one side of the rectangle, and the height is the perpendicular distance from the base to the opposite side.
Example 1
Find the area of a rectangle with length 5 cm and width 3 cm.
Solution
Length (L) = 5 cm
Width (W) = 3 cm
Area = \(Length \times Width\)
Area = \(5 \ cm \times 3 \ cm\)
Area = \(15 \ cm^2\)
\(\therefore\) the area of the rectangle is 15 \(cm^2\).
Remember: Length is the same as the base and the Width is the same as the perpendicular height.
A triangle can be thought of as half of a rectangle. To see this:
\(1.\) Draw a rectangle and label the base and the height .
\(2.\) Draw a diagonal line from one corner of the rectangle to the opposite corner. This divides the rectangle into two equal triangles.
This is shown below:
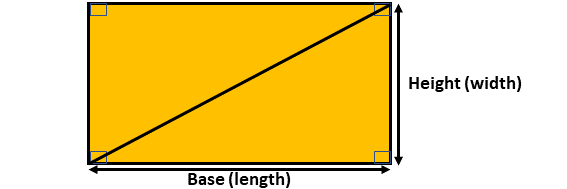
From the diagram above, it can be observed that Each triangle occupies exactly half the area of the rectangle.
We can therefore say, that the area of one triangle is half of the area of the rectangle or a parallelogram .
Mathematically;
Area of rectangle = Base \(\times\) Height
\(\therefore \) Area of triangle is given as\[\frac{1}{2} \times base \times height\]
Always remember that the height is the perpendicular height to the base.
Example 2
If the base of a triangle is 8 cm and the height is 5 cm, find the area of the triangle.
Solution
Base = 8 cm
Height = 5 cm
Area of triangle = \(\frac{1}{2} \times base \times height\)
\(\Rightarrow\) Area of triangle = \(\frac{1}{2} \times 8 \ cm \times 5 \ cm\)
\(\Rightarrow\) Area of triangle = \(4 \ cm \times 5 \ cm\)
\(\Rightarrow\) Area of triangle = \(20 \ cm^2\)
\(\therefore\) the area of the triangle is 20 \(cm^2\).
Example 3
A triangle has a base of 6 cm and a height of 4 cm. Find its area.
Solution
Base = 6 cm
Height = 4 cm
Area of triangle = \(\frac{1}{2} \times base \times height\)
\(\Rightarrow\) Area of triangle = \(\frac{1}{2} \times 6 \ cm \times 4 \ cm\)
\(\Rightarrow\) Area of triangle = \(3 \ cm \times 4 \ cm\)
\(\Rightarrow\) Area of triangle = \(12 \ cm^2\)
\(\therefore\) the area of the triangle is 12 \(cm^2\).
Example 4
A parallelogram has an area of 48 \(cm^2 \). If it is divided into two triangles by a diagonal, find the area of one triangle.
Solution
Area of parallelogram = \(48 \ cm^2 \)
Area of 1 triangle = \(\frac{1}{2}\) of parallelogram's area
\(\Rightarrow\) Area of triangle = \(\frac{1}{2} \times 48 \ cm^2\)
\(\Rightarrow\) Area of triangle = \(24 \ cm^2\)
\(\therefore\) the area of one triangle is \(24 \ cm^2\).
Watch a walk-through of the solution in the video. Kindly subscribe to help us.
Example 5
A triangle has a base of 8 cm and a height of 6 cm. Find its area.
Solution
Base = 8 cm
Height = 6 cm
Area of triangle = \(\frac{1}{2} \times base \times height\)
\(\Rightarrow\) Area of triangle = \(\frac{1}{2} \times 8 \ cm \times 6 \ cm\)
\(\Rightarrow\) Area of triangle = \(4 \ cm \times 6 \ cm\)
\(\Rightarrow\) Area of triangle = \(24 \ cm^2\)
\(\therefore\) the area of the triangle is 24 \(cm^2\).
Watch a walk-through of the solution in the video. Kindly subscribe to help us.
-
A triangle has a base of 7 cm and a height of 5 cm. Calculate its area.
-
A rectangle has a base of 10 cm and a height of 8 cm. If a triangle is formed by cutting the rectangle diagonally, what is the area of the triangle?
-
A parallelogram has a base of 12 cm and a height of 6 cm. What is the area of one triangle formed by its diagonal?
-
A triangle has an area of \(30 cm^2\), and its base is 12 cm. What is its height?
-
A triangle has a base of 10 m and a height of 6 m. If both the base and height are doubled, what will be the new area of the triangle?
Test yourself on what you have learnt so far. Click on the link below when you are ready.
Kindly contact the administrator on 0208711375 for the link to the test.
For sponsorship or advertisement kindly call or whatsapp on 0208711375 or 0249969740.