In our lesson on the relationship between the hypotenuse and the other two sides of a right-angled triangled triangle, we learnt that, given any right-angled triangle, the square of the hypotenuse is equal to the sum of the square of the other two sides.
That is, if the length of the hypotenuse is '\(c\)' and the length of the other two sides '\(a\)' and '\(b\)', then the Pythagorean Theorem states that: \[c^2 = a^2 + b^2\]
In this lesson, we will use the Pythagorean Theorem to solve questions with regards to the area of triangles.
Find below some examples on questions about the area of triangles that involve the use of the Pythagorean Theorem, and try your hands on the exercises to improve on your confidence in solving questions.
Example 1
A boat travels 2m South and then 9m East. How far is the boat from its starting point?
Example 2
Yeboah hangs a picture frame of width 15cm on the wall. The distance from the nail to the edge of the picture frame is 10cm.
\((a)\) Find the length of the wire used to hang the picture frame.
\((b)\) Find the area of the triangle.
Example 3
A ladder leans against a vertical wall of height 13m. If the foot of the ladder is 6m away from the wall, calculate the length of the ladder
Example 4
The length of a side of an equilateral triangle is 12cm. Find
\((a)\) the height of the triangle
\((b)\) the area of the triangle
\((c)\) the perimeter of the triangle
Example 5
Find the perimeter of the shape below.
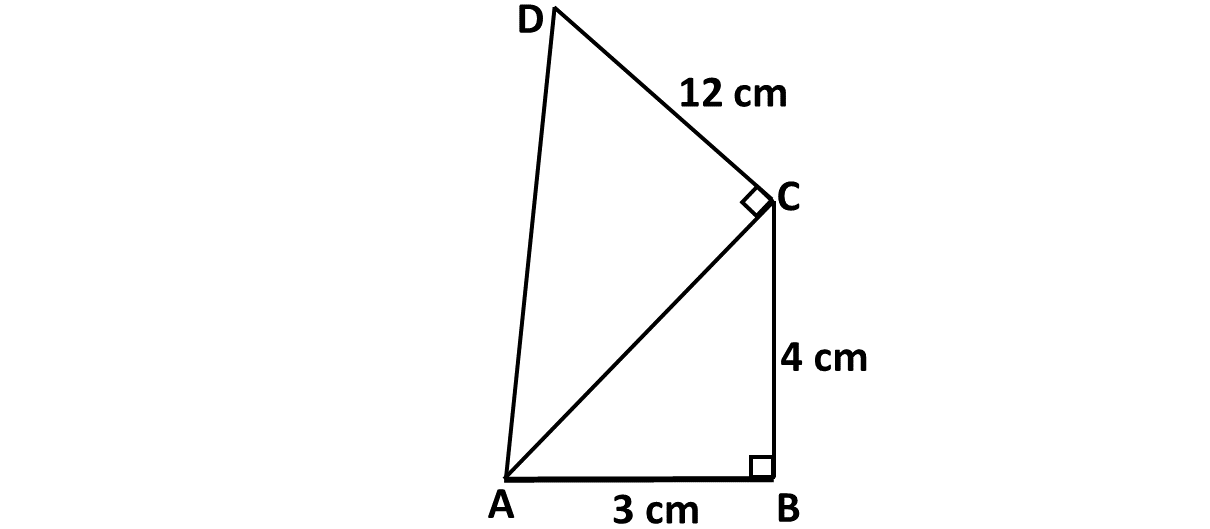
Solve the following:
-
In \(\triangle XYZ\), \(\lvert XZ \rvert = 13 \ cm\), \(\lvert XY \rvert = 12 \ cm\) and \(\angle XYZ = 90^\circ\). Find \(\lvert YZ \rvert\) if the area of the triangle is \(30 \ cm^2.\)
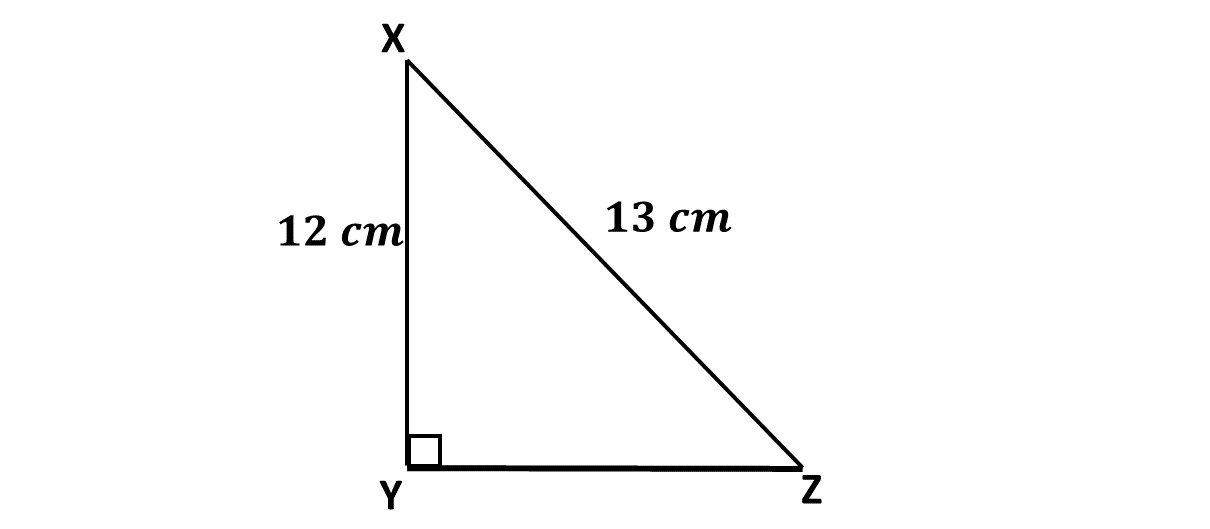
-
Find the area of the triangle below.
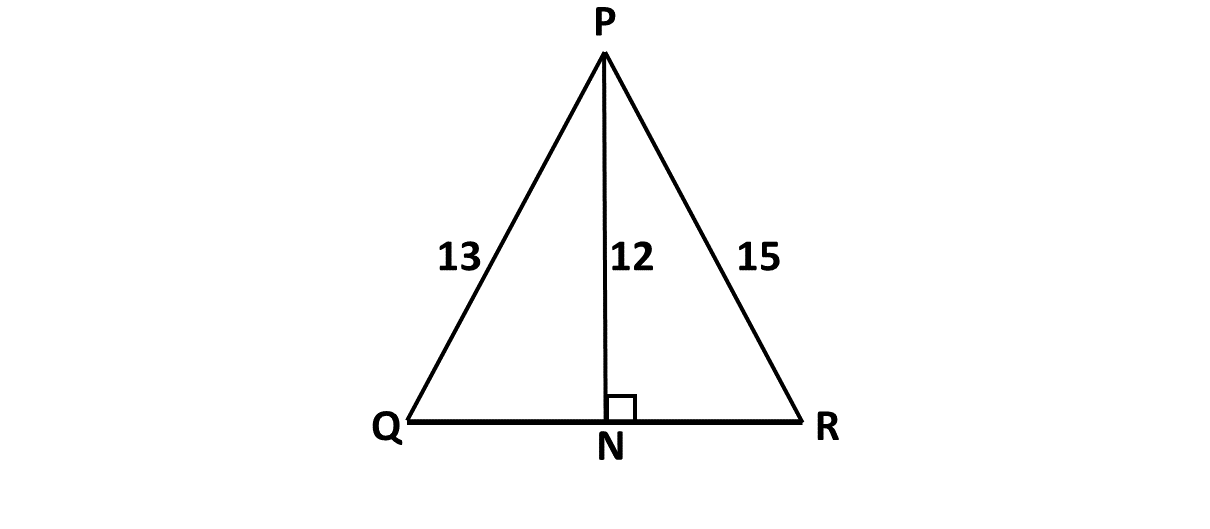
-
A right-angled triangle has one leg measuring 9 cm and the other leg measuring 12 cm.
\((i)\) Calculate the hypotenuse.
\((ii)\) Find the perimeter of the triangle.
\((iii)\) Find the area of the triangle.
-
A rectangle has a diagonal of 15 m and one side measuring 9 m.
\((i)\) Find the length of the other side.
\((ii)\) Calculate the perimeter and the area of the rectangle.
-
A right-angled triangle has a perimeter of 60 cm. If the two shorter sides are 18 cm and 24 cm,
\((i)\) Find the hypotenuse.
\((ii)\) Calculate the area of the triangle.
Test yourself on what you have learnt so far. Click on the link below when you are ready.
Kindly contact the administrator on 0208711375 for the link to the test.
For sponsorship or advertisement kindly call or whatsapp on 0208711375 or 0249969740.