In our lesson on the relationship between the hypotenuse and the other two sides of a right-angled triangled triangle, we learnt that, given any right-angled triangle, the square of the hypotenuse is equal to the sum of the square of the other two sides.

That is, if the length of the hypotenuse is '\(c\)' and the length of the other two sides '\(a\)' and '\(b\)', then the Pythagorean Theorem states that: \[c^2 = a^2 + b^2\]

In this lesson, we will use the Pythagorean Theorem to solve more questions with regards to right-angled triangles.

---

Find below some examples on questions about the Pythagorean Theorem, and try your hands on the exercises to improve on your confidence in solving questions.

---

Example 1

[BECE 1995]

Find the length of \(PQ\) in the triangle \(PQR\).

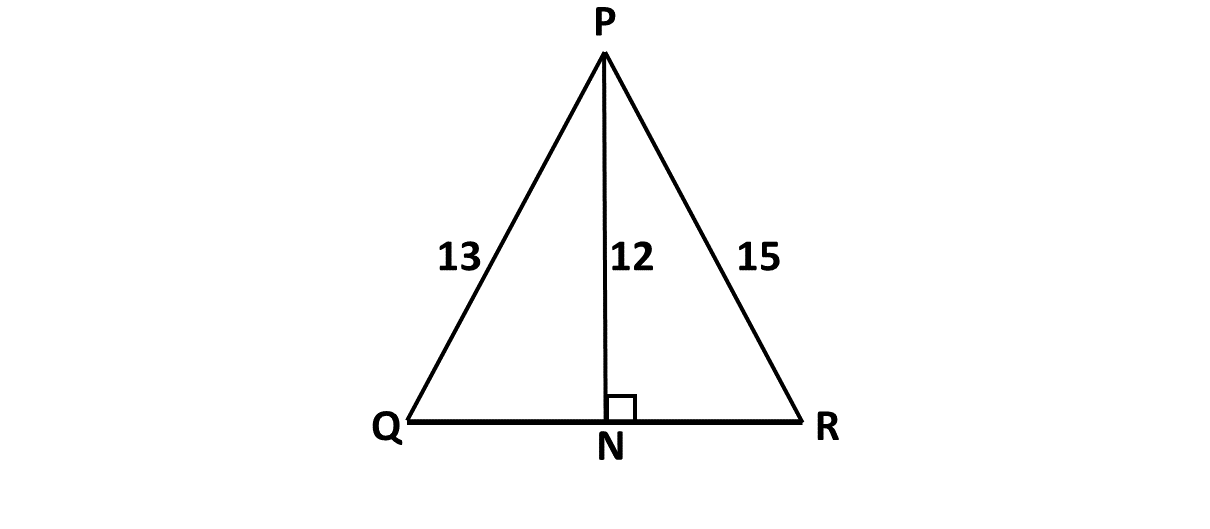
Show Solution

---

Example 2

[BECE 1998]

In the triangle, angle \(RST\) is \(90^\circ\). \(RS = 4 cm\) and \(ST = 3cm\). what is the length of \(RT\)?

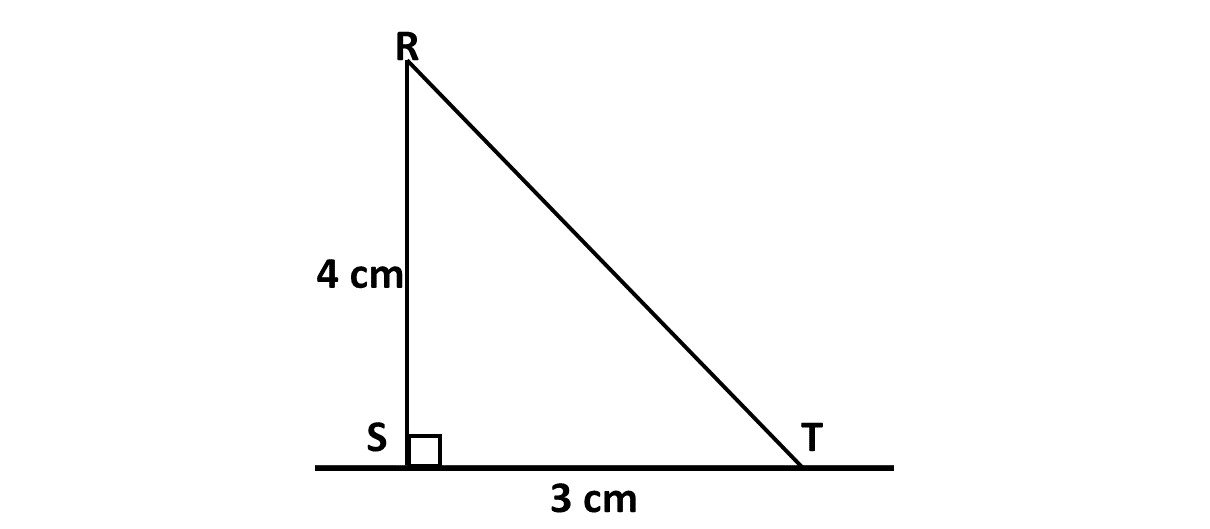
Show Solution

---

Example 3

[BECE 2000]

In the diagram, \(MNO\) is a right-angled triangle, \(MO = 13 cm\) and \(MN\) is \(5 cm\).

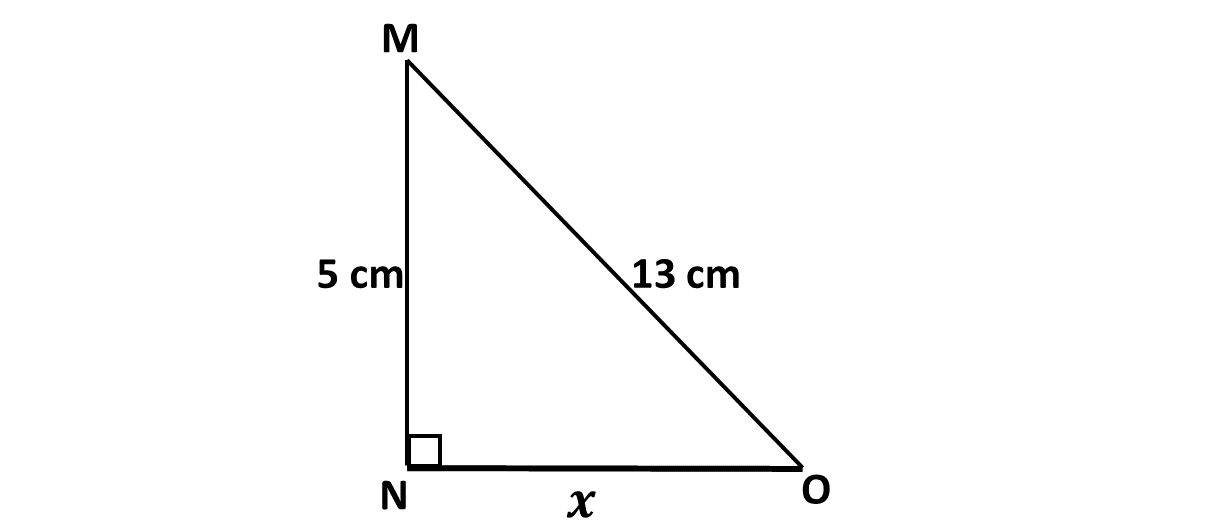
Find the value of \(x\).

Show Solution

---

Example 4

[BECE 2002B]

\(PQR\) is a right-angled triangle. The area of the triangle is \(6 \ cm^2\) and \(QR = 3 \ cm\). Find \(\lvert PR \rvert\).

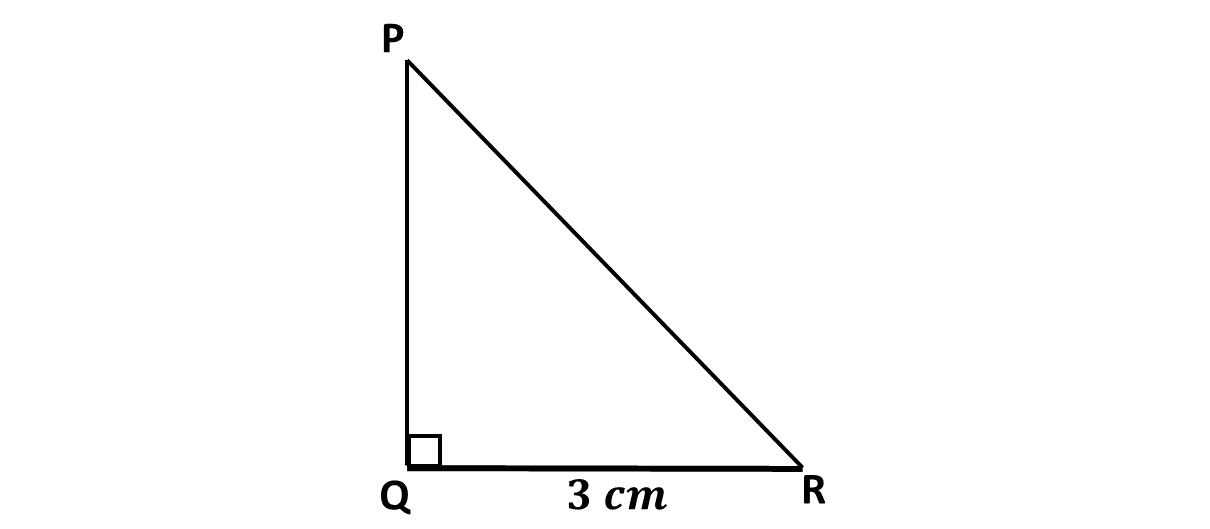
Show Solution

---

Example 5

[BECE 2003]

In triangle \(XYZ\), angle \(XZY = 90^\circ\), \(\lvert XY \rvert = 13 cm\) and \(\vert YZ \rvert = 5 cm.\) What is the length of \(XZ\).

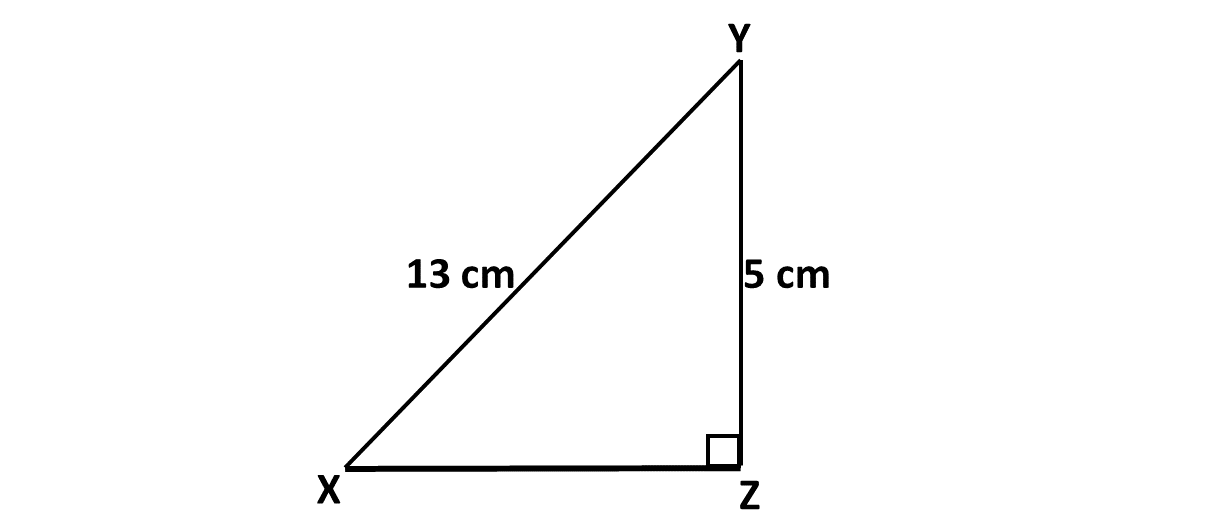
Show Solution

---

Solve the following questions.

1. [BECE 1990]

   In \(\triangle XYZ\), \(\lvert XZ \rvert = 13 \ cm\), \(\lvert XY \rvert = 12 \ cm\) and \(\angle XYZ = 90^\circ\). Find \(\lvert YZ \rvert\), if the area of the triangle is \(30 \ cm^2\).

   



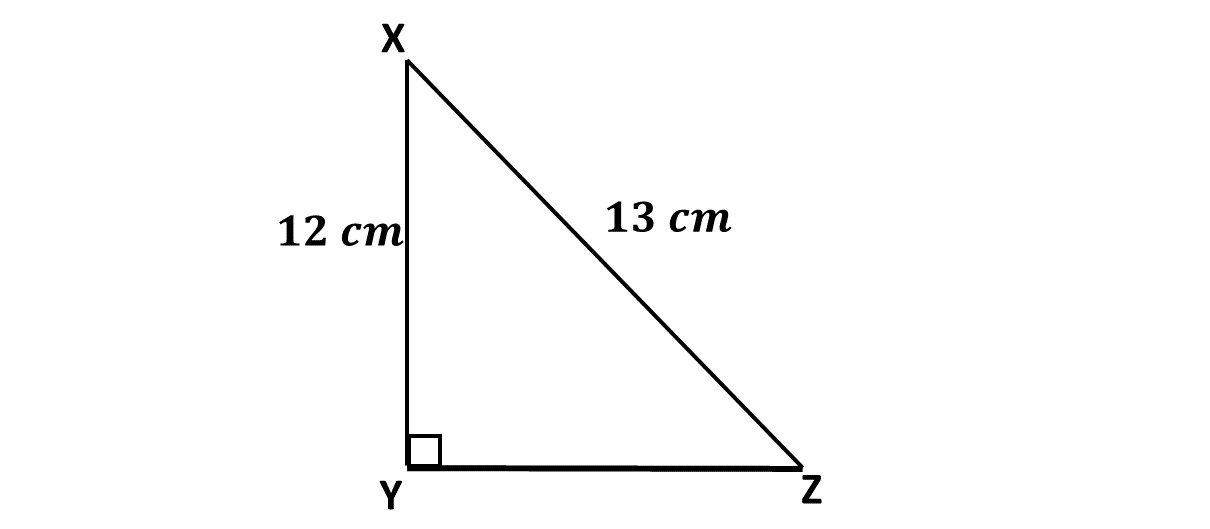
2. [BECE 1994]

   In triangle \(ABC\), \(\lvert AB \rvert = \lvert BC \rvert = 5 \ cm\) and \(\lvert AC \rvert = 8 \ cm\). Find \(\lvert BD \rvert\).

   



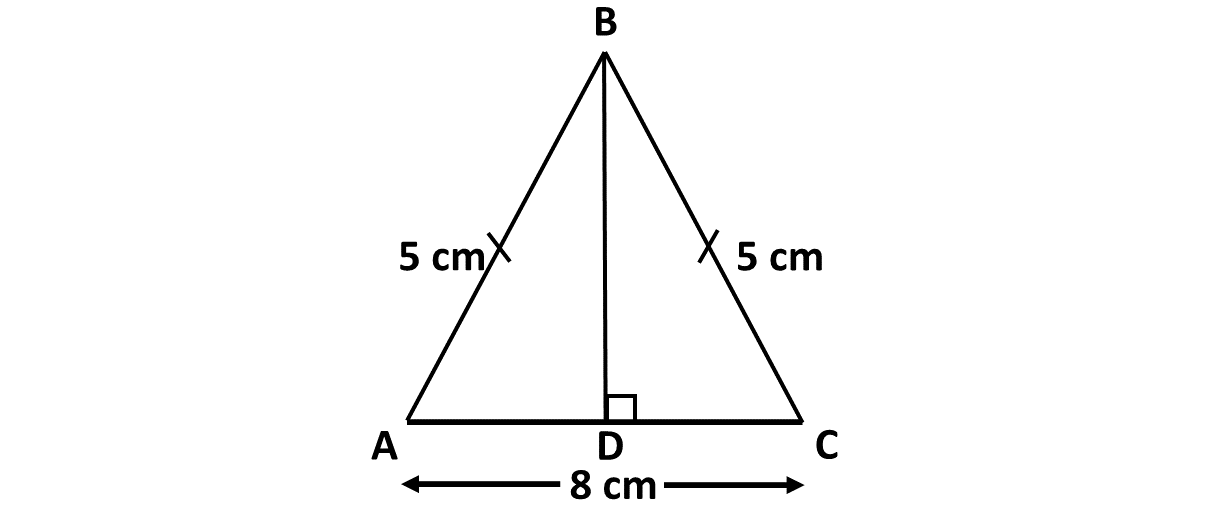
3. [BECE 1994, Section B Question 2a]

   A ladder leans against a wall. The end of the ladder touches the wall 12 m from the ground. The foot of the ladder is 9 m away from the foot of the wall. What is the length of the ladder?




4. Find the perimeter of the shape below.

   



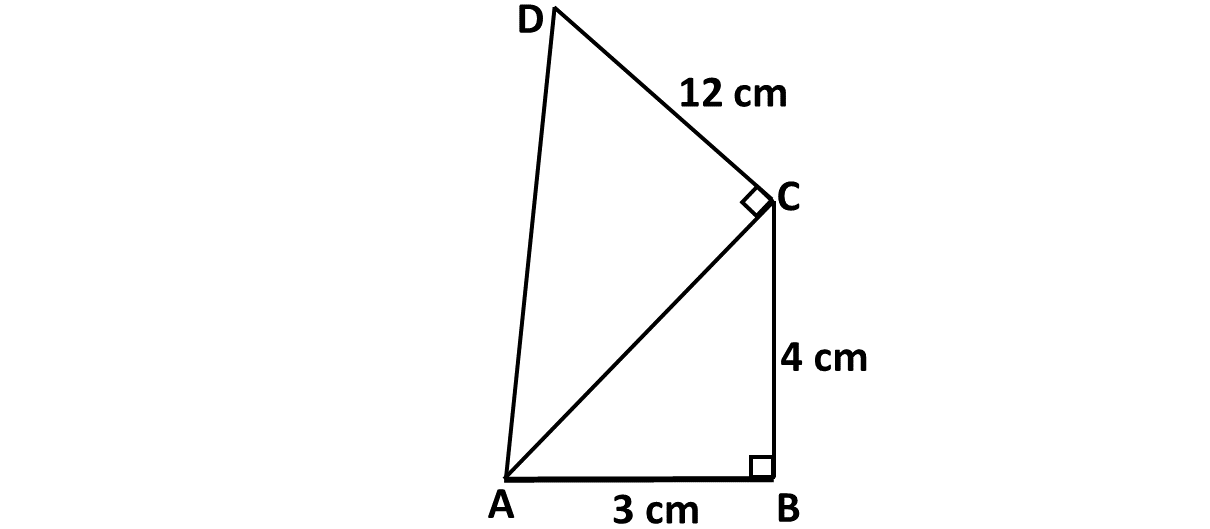
5. An isosceles triangle has equal sides, 6cm long and a base of 4cm long. Find the altitude of the triangle.

---

Test yourself on what you have learnt so far. Click on the link below when you are ready.

Kindly contact the administrator on 0208711375 for the link to the test.

---

For sponsorship or advertisement kindly call or whatsapp on 0208711375 or 0249969740.