In our lesson on the circumference of a circle, we learnt that the circumference is the distance around the circle, or the length of the boundary of any given cirlce.
We also learnt that, whenever you divide the circumference of any given circle by its diameter, you obtain a constant \(\pi\), pronounced as ('pie').
That is; \[\frac{C}{d} = \pi\]
We used this relationship between the diameter and the circumference of a circle to write the two formulars for the circumference of a circle. We found that;
\(*\) when the diameter is known:
Circumference, \( C = \pi d \)
\(\) when the radius is known:
Circumference, \(C = 2 \pi r\)
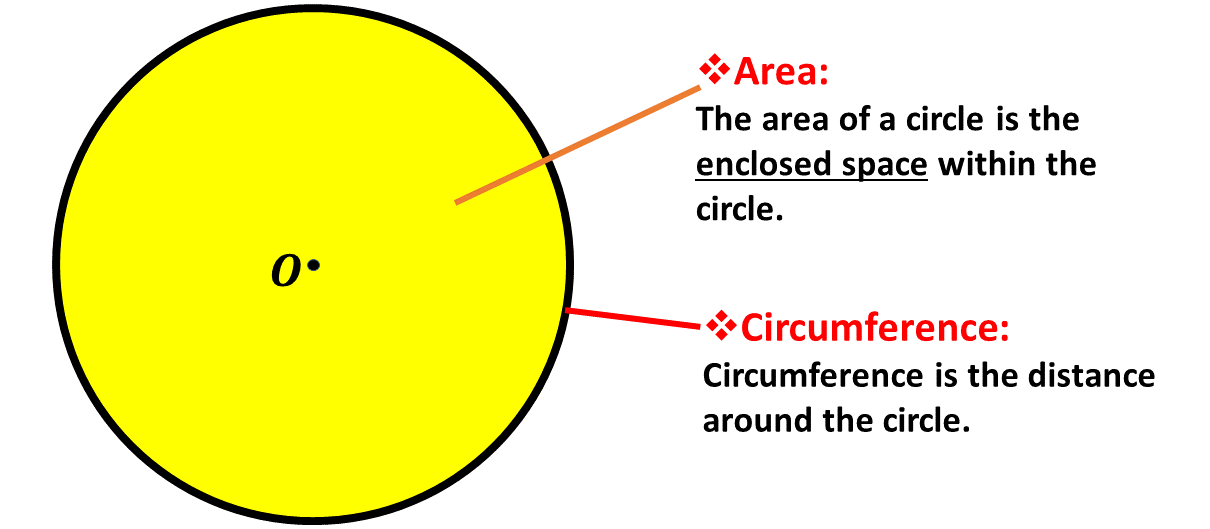
In this lesson, we will learn about the area of a circle. That is, the space enclosed by the boundary of the circle. In the diagram below, the area of the circle is the space coloured yellow.
We can divide the circle into a number of sectors, say 16, as illustrated in the diagram below:
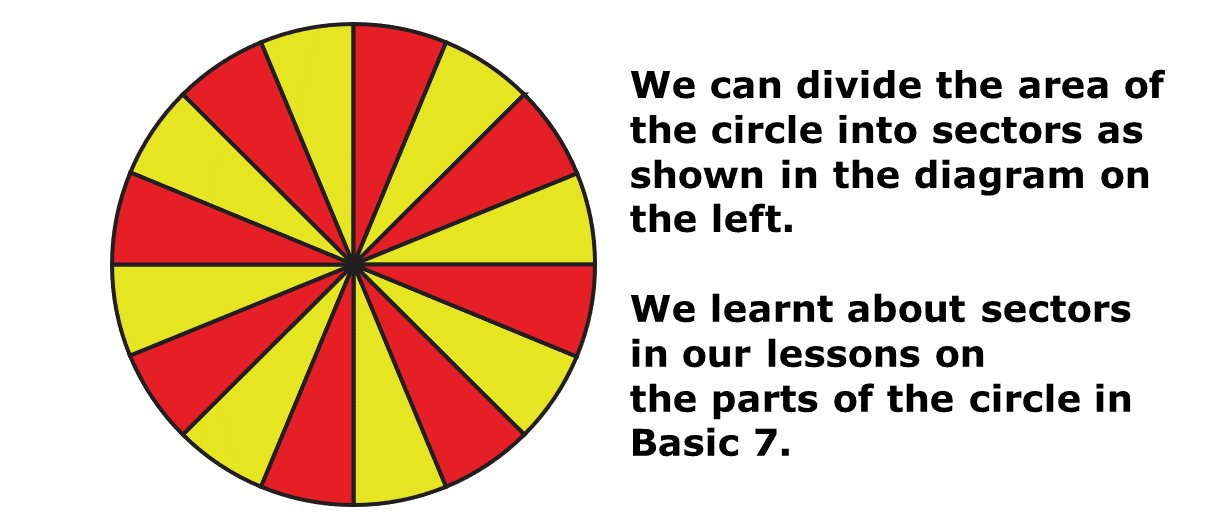
We can then group the yellow sectors and the red sectors, as done in the diagram below.
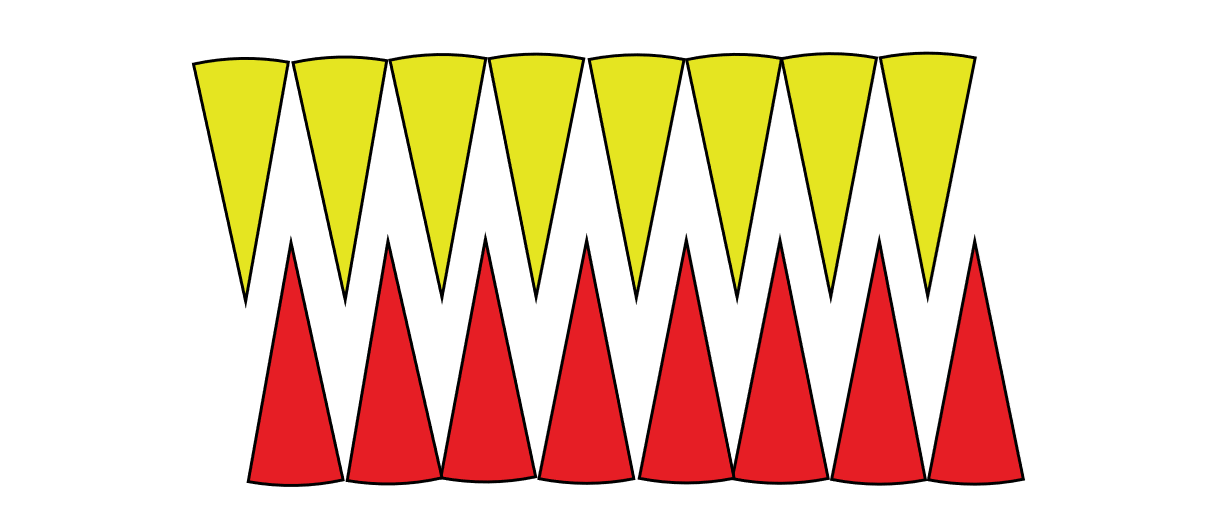
These smaller sectors can then be rearranged to form a shape that resembles a parallelogram. This is also illustrated in the diagram below.
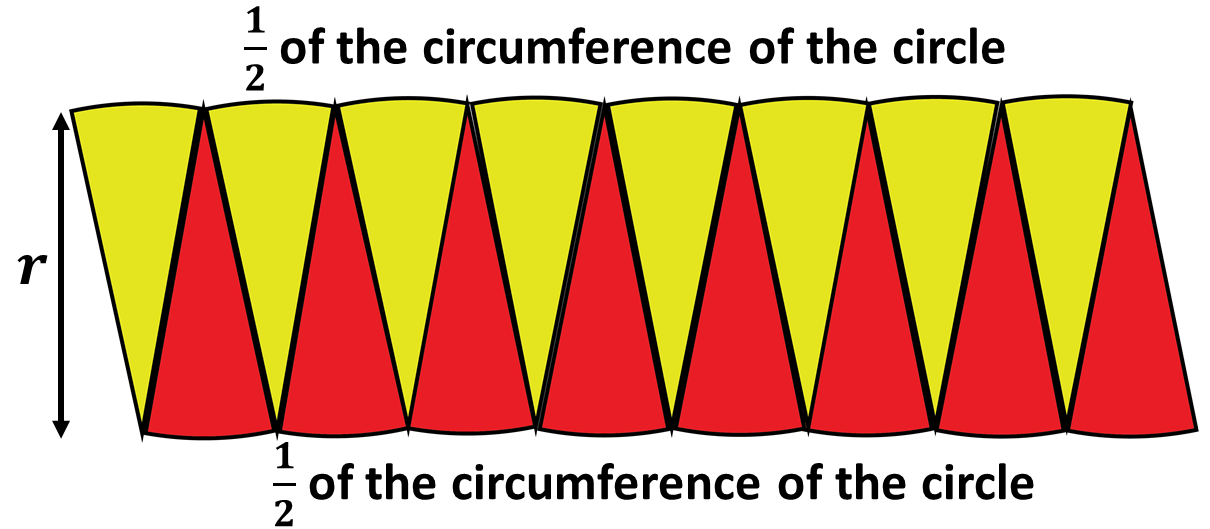
From the diagram above, it can be seen that, the top length of the parallelogram is half of the circumference of the circle. This is also true for the bottom length of the parallelogram.
Also the width of the parallelogram is the same as the radius of the circle.
That is,
Length of parallelogram = \(\frac{1}{2}\) of Circumference
but the circumference, \(C = 2 \pi r\)
Substituting the formular of the circumference into the length of the parallelogram gives:
Length \(= \frac{1}{2} \times 2 \pi r\)
\(\Rightarrow\) Length \(= \pi r\)
From the diagram, the width is \(r\), as stated above.
Formular for the area of a parallelogram is given as \[Length (L) \times Width (W)\]
Substituting, we have the area of the parallelogram above, which is the same as the area of our initial circle as \[Area = \pi r \times r\]
Which implies \[Area = \pi r^2\]
From our deduction above we can therefore say that given the radius the area of any circle can be calculated using the formulae below:
Area of a Circle \(=\mathbf{\pi r^2}\)
Where \(r \Rightarrow\) radius and
\(\pi \Rightarrow \frac{22}{7}\) or 3.14159 correct to 5 decimal places
Note: It would be useful to memorize this formular as you would be required to reproduce it in your calculations.
Let us now use the formula for finding the area of a circle to solve questions. Remember to practice more questions to build your confidence.
Example 1
Find the area of a circle whose radius is 14cm (Take \(\pi = \frac{22}{7}\))
Solution
Example 2
Find the area of a semi-circle whose radius is 7cm (Take \(\pi = \frac{22}{7}\))
Solution
Example 3
Two circles have a common centre; the small circle has radius 7cm, the big circle has radius 14cm. Find the shaded area. (Take \(\pi = \frac{22}{7}\))
Solution
Example 4
A cylinder has diameter 4 cm and length 14 cm. Calculate the area of the base. (Take \(\pi = \frac{22}{7}\))
Solution
Example 5
Two radii meet at an angle of \(60^\circ\) at the center of a circle. Calculate the area of the minor sector the two radii create, if the radius of the circle is 21 cm. (Take \(\pi = \frac{22}{7}\))
Solution
Test yourself on what you have learnt so far. Click on the link below when you are ready.
Kindly contact the administrator on 0208711375 for the link to the test.
To advertise on our website kindly call on 0208711375 or 0249969740.