Angles help us to understand shapes, structures, and the relationships between lines. In this lesson, we will explore two important types of angles: alternate angles and corresponding angles. These two angles occur when a tranversal intersects two or more parallel lines.
In the diagram below, line segments \(AB\), \(CD\) and \(EF\) are called parallel lines.
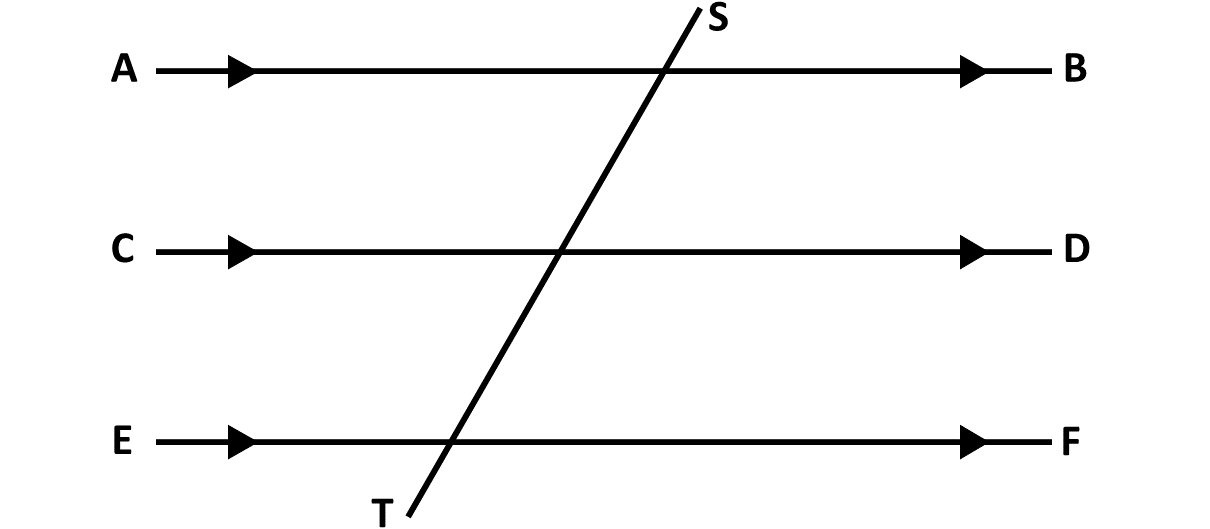
Parallel lines are lines that lie in the same plane and never intersect, no matter how far they are extended. In other words, parallel lines are lines that are always the same distance apart and never touch.
Also, in the diagram above, line segment \(TS\) is called a tranversal. A transversal is a line that intersects two or more other parallel lines.
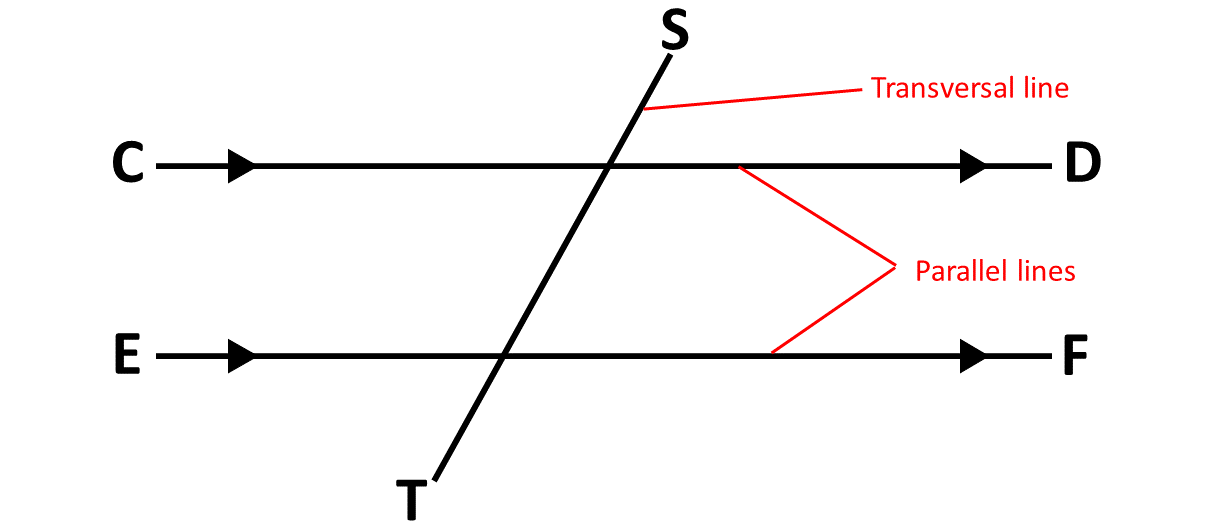
Alternate angles are pairs of angles that are on opposite sides of a transversal (a line that intersects two other lines). They are called "alternate" because they alternate with each other around the transversal.
Theorem:
Alternate angles are equal.
Consider the diagrams below:
When a tranversal intersects two or more parallel lines, the alternate angles are formed in the shapes outlined in red in the diagrams below.
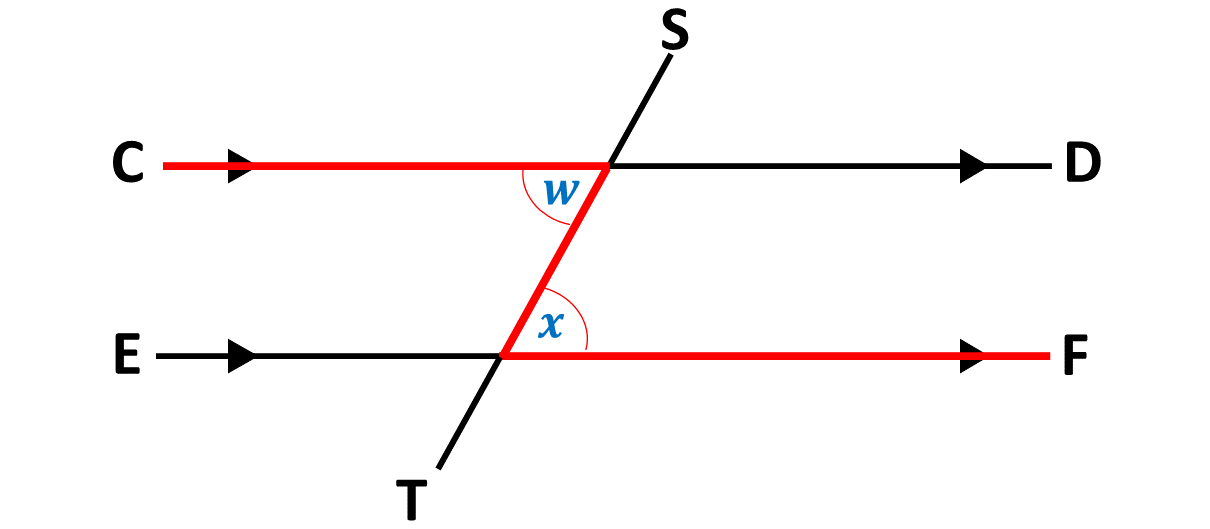
In the shape above, we say that \(\angle w\) and \(\angle x\) are alternate angles.
\(\therefore \) \(\angle w\) \(=\) \(\angle x\)
See how the shape above resembles the letter \(\mathbf{Z}\)?
Also:
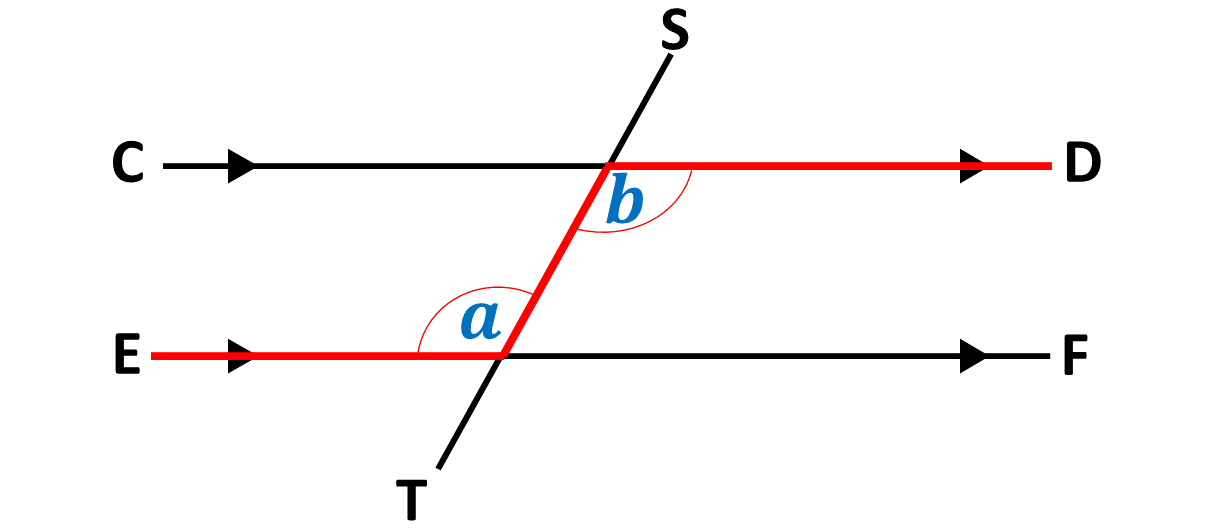
In the shape above, we say that \(\angle a\) and \(\angle b\) are alternate angles.
\(\therefore \) \(\angle a\) \(=\) \(\angle b\)
Always remember, that altenate angles are equal.
Example 1
Solution
Example 2
Solution
Example 3
Solution
Example 4
Solution
Example 5
Solution
Corresponding angles also occur when a transversal intersects two parallel lines. These angles are located on the same side of the transversal but at different positions relative to the parallel lines.
Theorem:
Corresponding angles are equal.
Two angles are corresponding if:
1. One angle is located above or below one parallel line and
2. the other angle is located above or below the other parallel line, in the same relative position.
Consider the diagrams below:
If a transversal intersects two parallel lines, the angles marked as \(\alpha\) (above the first line) and \(\beta\) (above the second line) are corresponding angles as indicated in the diagram below.
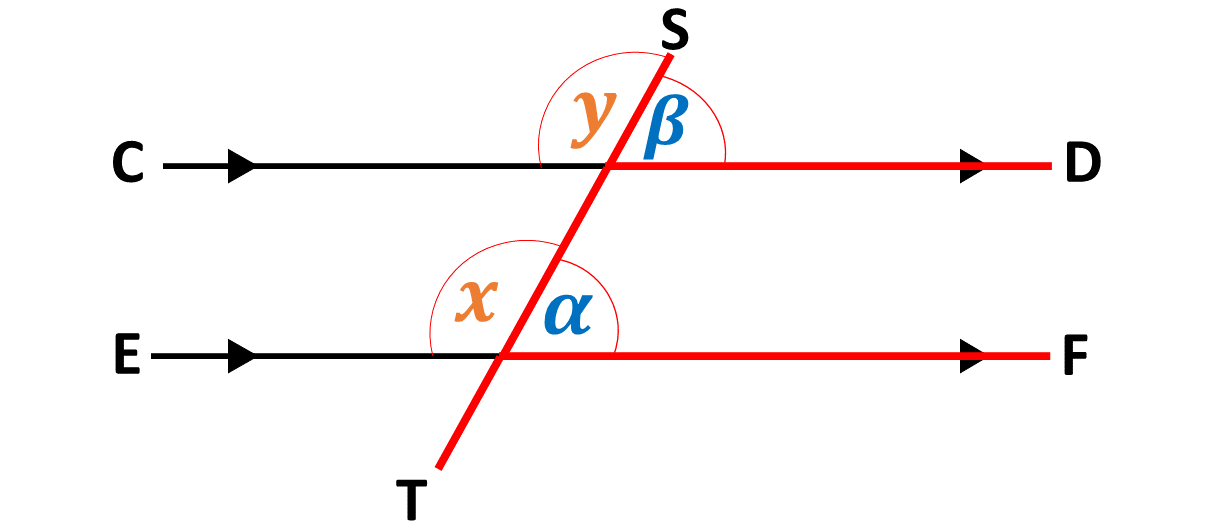
\[\angle \alpha = \angle \beta\]
Also, \(\angle x\) and \(\angle y\) are corresponding angles. It follows therefore that;
\[\angle x = \angle y\]
Let's look at the corresponding angles formed on the other side of the two parallel lines in the diagram below:
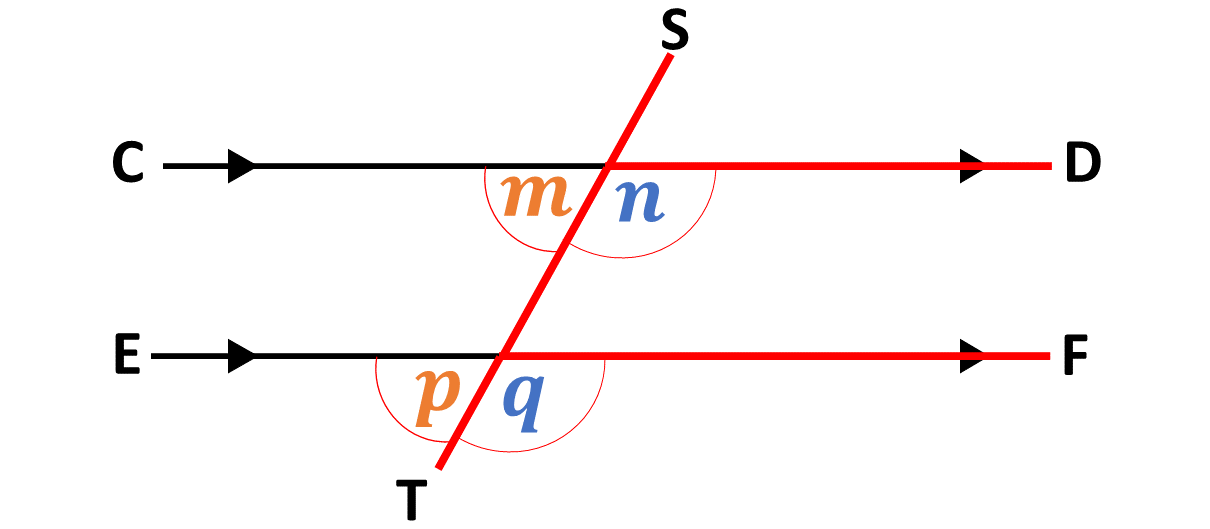
In the diagram above, \(\angle p\) and \(\angle m\) are said to be corresponding angles. The angles \(q\) and \(n\) are also corresponding angles.
It therefore follows that,
\[\angle p = \angle m\] and
\[\angle q = \angle n\]
Always remember, that corresponding angles are equal.
Example 1
Solution
Example 2
Solution
Example 3
Solution
Example 4
Solution
Example 5
Solution
Test yourself on what you have learnt so far. Click on the link below when you are ready.
Kindly contact the administrator on 0208711375 for the link to the test.
To advertise on our website kindly call on 0208711375 or 0249969740.