Place value refers to the value of a digit based on its position within a number. Each digit in a number has a different place value depending on its position from right to left.
\(*\) The rightmost digit is in the ones place \(\Rightarrow\) Ones
\(*\) The next digit to the left is in the tens place \(\Rightarrow\) Tens
\(*\) The next digit to the left is in the hundreds place \(\Rightarrow\) Hundreds
\(*\) And so on, increasing by powers of 10 as you move to the left.
This pattern can extend to larger numbers, and to smaller fractions using decimals, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, etc.
To know the value of a particular digit in a number, we can expand the number as shown in the example below:
Example 1
What is the value of the underlined digit in the number 489,000?
Solution
Let's first use our knowledge of addition of numbers to expand the given number as below.
\(\Rightarrow 489,000 =\)\(\ 400,000 + \mathbf{80,000} + 9,000\)
It implies, that the value of the underlined digit is \(80,000\) (eighty thousand).
Use addition to expand the numbers below in order to find the value of the underlined digits.
-
123,432,009
-
89,009,092
-
770,098,990,211
-
100,100,111
-
80,783,090,391
Consider the place value table below.
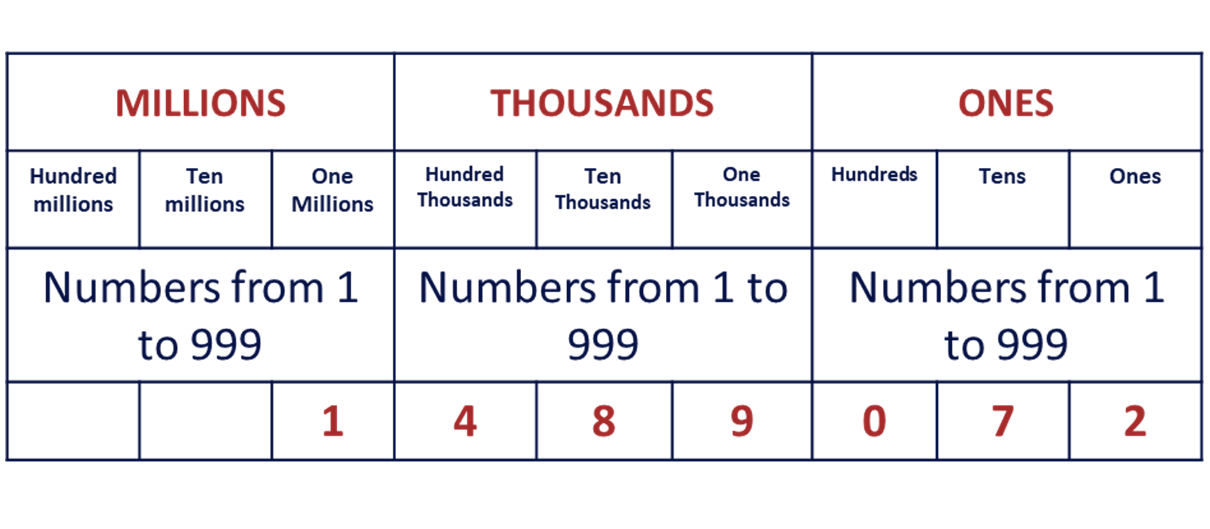
To easily read and write a given number, first, you need to know the place value of the individual digits within the number. Use the table above to help you learn how to read and write numbers by following the steps below:
\(*\) STEP 1
Starting from right (the ones column) to the left, fill the boxes with the digits of the number, as shown above.
\(*\) STEP 2
To read the number or write it in words, you will need to consider the bigger columns, that is, millions, thousands and ones. Each column take values from 1 to 999. Under the millions column, we have the number 1, hence you say, “one million”.
NB: After writing the word million, you need to bring the comma (,).
\(*\) STEP 3
Now move to the bigger thousands column. The number under the bigger thousands column is 489 (four hundred and eighty-nine). You say or write, “four hundred and eighty-nine thousand”.
\(*\) STEP 4
After writing the word “thousand” you would have brought a comma (,) but the next number under the hundreds column is zero (0), so omit the comma and write “and” instead. Now write the number under the bigger 'ones' column, 72 (seventy-two).
So here you say or write, “and seventy-two”
Putting it all together, we have, “One million, four hundred and eighty-nine thousand and seventy-two.”
NOTE
-
Whenever you write the word “hundred,” the next word should be “and.”
-
Remember to bring the comma (,) after writing the bigger column words:
\((i)\) billion
\((ii)\) million
\((iii)\) thousand, etc.
-
When the next number after the comma is zero (0), omit the comma and write “and” instead.
Example 2
Write the number \(1,025,495,325\) in words.
Solution
Let's use the place value table we constructed.

\(1,025,495,325 \Rightarrow \) One billion and twenty-five million, four hundred and ninety-five thousand, three hundred and twenty-five.
Example 3
Write the number \(1,000,276,009\) in words.
Solution
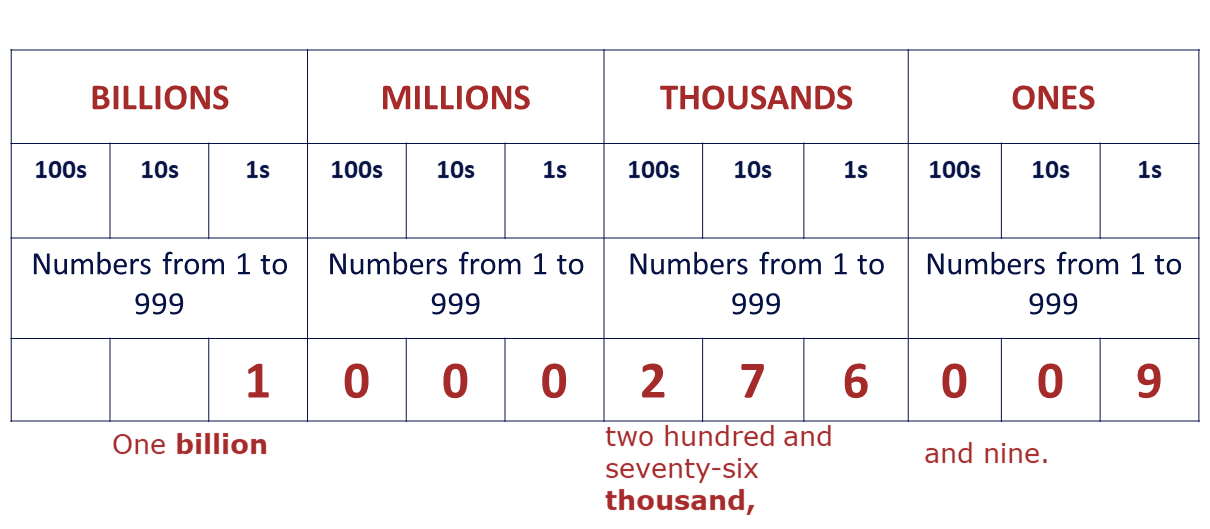
\(1,000,276,009 \Rightarrow \) One billion, two hundred and seventy-six thousand and nine.
NB: The place value of the numbers at the bigger million column is zero (0), hence we can ignore the “comma (,) - and” rule.
Example 4
Write the number \(1,000,086,019\) in words.
Solution
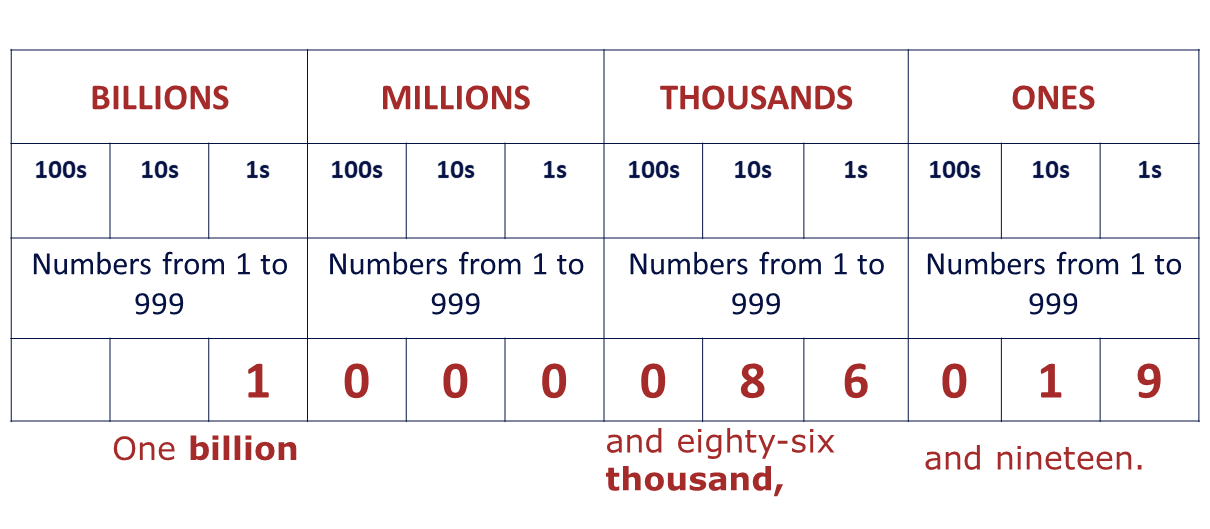
\(\therefore 1,000,086,019 \Rightarrow\) One billion and eighty-six thousand and nineteen.
Sometimes, to prevent using the word “and” twice in writing the number, we can replace the first “and” with the comma (,).
Hence, we can also write the above number as below:
\(1,000,086,019 \Rightarrow\) One billion, eighty-six thousand and nineteen.
Write the following numbers in words.
-
3,900,089
-
78,000,987,098
-
567,890,009,007
-
3,098,067,907
-
45,704
Example 5
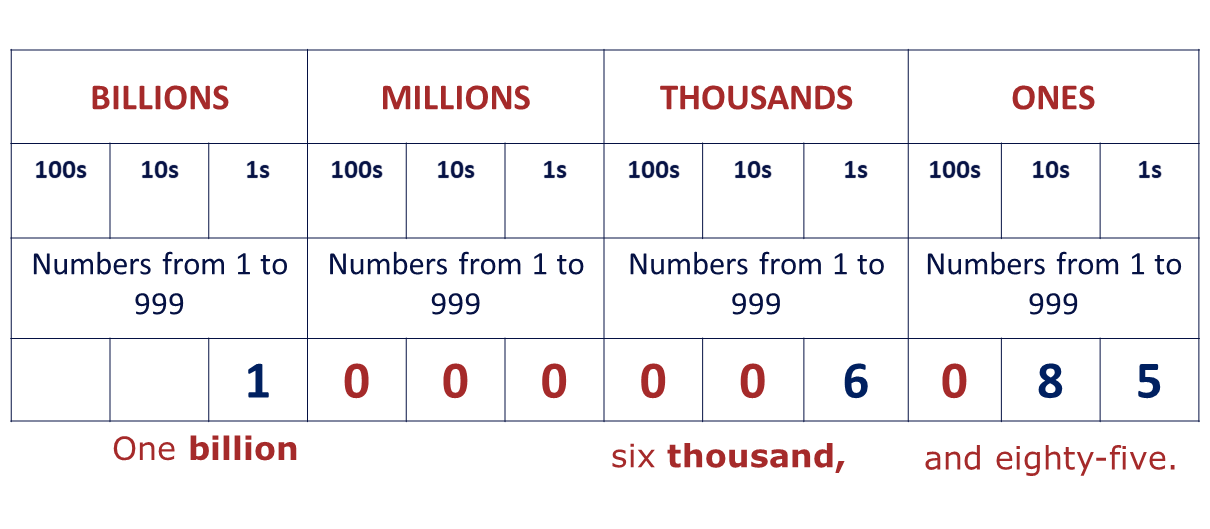
Write one billion, six thousand and eighty-five in figures.
Solution
Let's write the words under our columns, billions, millions, thousands and ones as below:
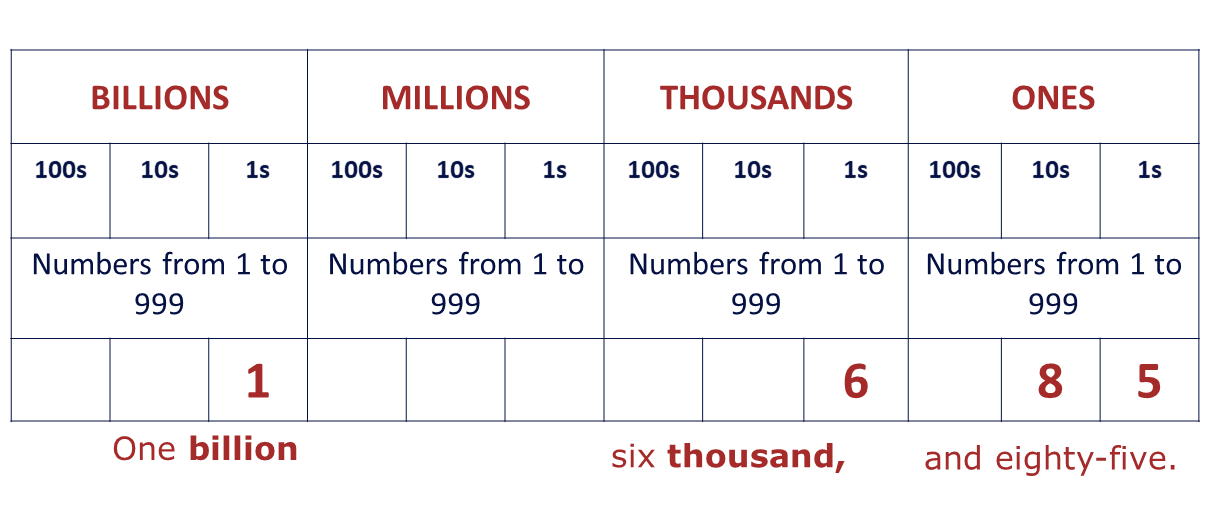
Remember that each bigger column takes values from 1 (one) to 999 (nine hundred and ninety-nine).
Follow the steps below to complete the table.
\(*\) STEP 1
Write the words under the table as shown above and insert the numbers that were mentioned in their respective places.
\(*\) STEP 2
Insert the number zero (0) at all the other places in between the numbers, where there are no numbers as below:
\(*\) STEP 3
Write the number down. Counting from right to left, put a comma (,) after every third (3rd) count as below:
\(1,000,006,085\)
Hence the number one billion, six thousand and eighty-five in figures is \(1,000,006,085\).
Write the numbers below in figures:
1. Seventeen thousand and five.
2. Nine hundred and eighty-five billion, two hundred and seventy-seven million, three hundred and twenty-five thousand and ninety-six.
3. One trillion and thirty-eight billion, five hundred and forty-six million, six hundred thousand and four.
4. Sixteen thousand, two hundred and nineteen.
5. One million and forty-eight.
Currency notes, whether they're pounds, dollars, euros, Ghana cedi or any other type, usually have a unique identifier known as a serial number. This serial number is a combination of letters and numbers that is printed on each note to ensure that no two notes are exactly alike.
Serial numbers help in identifying counterfeit notes, keeping records in banks and other financial companies.
They usually consist of two (2) parts:
-
Prefix letters:
-
Numeral Part:
Usually 1 or 2 letters at the beginning of the serial number.
Digits that follow the letter(s).
Consider the currency notes below. Read the numeral part of the notes in words.

The numeral part of the dollar currency note above is 41524052. Using the steps we learnt in reading or writing figures in words, the numeral part of the serial number will be read as below:
\(41524052 \Rightarrow \) Forty-one million, five hundred and twenty-four thousand and fifty-two.

The numeral part of the Ghana Cedi currency note above is 238505. Using the steps we learnt in reading or writing figures in words, the numeral part of the serial number will be read as below:
\(238505 \Rightarrow \) Two hundred and thirty-eight thousand, five hundred and five.
Note:
When the number zero (0) has the highest place value in any written number, it is ignored. For instance, the numeral part on the Ghana cedi note above is 0238505.
Write the numeral part of the currency notes below in words.
1. AD1567258
2. TM1563451
3. TH1547454
4. TJ1667451
5. TP0567452
Test yourself on what you have learnt so far. Click on the link below when you are ready.
Kindly contact the administrator on 0208711375 for the link to the test.
To advertise on our website kindly call on 0208711375 or 0249969740.