Complementary angles are two angles whose measures add up to 90 degrees. In other words, if the sum of the measures of two angles is 90°, they are complementary angles.
It can also be said that complementary angles are two angles whose sum is 90 degrees. These angles form a right angle when combined.
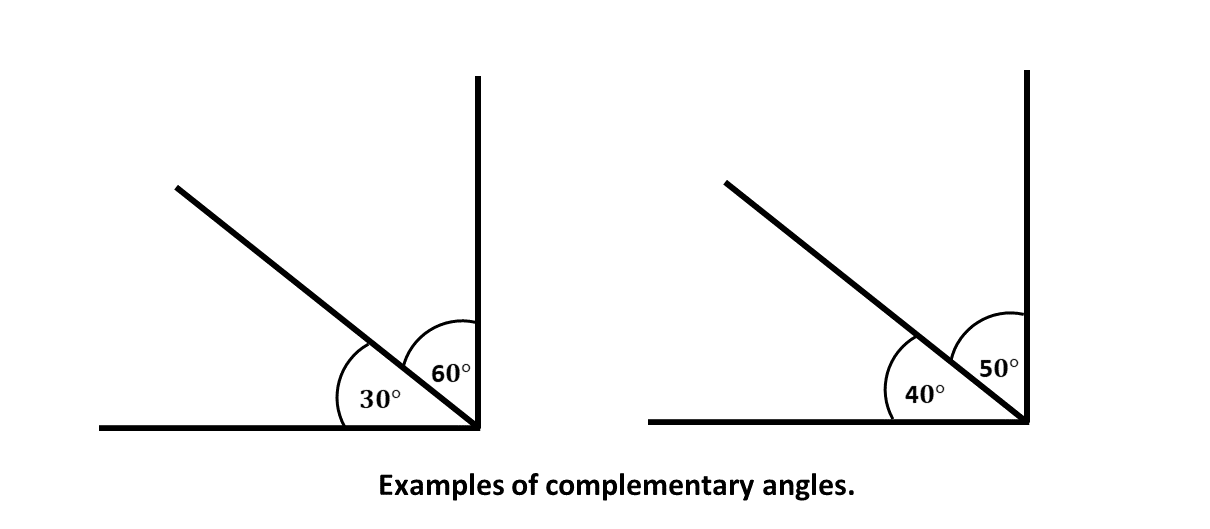
Example: If one angle is 40°, the other angle will be 50° (40° + 50° = 90°). The two angles are said to be complementary to each other.
Examples
Below are some examples of complementary angles.
-
Angle 1 = 30° and Angle 2 = 60° (30° + 60° = 90°)
-
Angle 1 = 45° and Angle 2 = 45° (45° + 45° = 90°)
-
Angle 1 = 20° and Angle 2 = 70° (20° + 70° = 90°)
-
Each angle is acute, as their measures are less than 90°.
-
If two angles are complementary, they can be adjacent or non-adjacent.
-
Complementary angles are not necessarily congruent.
Example 1
Angle A measures 35°. What is the measure of its complementary angle?
Answer:
Angle A \(= 35^\circ\)
Complementary angles add up to \(90^\circ\)
\(\therefore\) its complementary angle \(\Rightarrow 90^\circ - 35^\circ\)
\(\Rightarrow 55^\circ\)
\(\therefore\) the complementary angle to angle A is \(55^\circ\)
Try Work
1. Find the complementary angle of 65°.
2. Two angles are complementary to each other. If one of the angles is \(x\), what is the value of the other angle.
3. Two angles are such that, the first angle is three times the second angle. If the two angles are complementary, find the value of the bigger angle.
Answers
1. \(25^\circ\)
2. \((90 - x)^\circ\)
3. \(22.5^\circ\)
To advertise on our website kindly call on 0208711375 or 0249969740.