BECE 2025 | JHS Mathematics | The Let's Learn Project

GUIDE (BECE - 2025)

You have 60 minutes for each section. Try to work on your speed as you prepare towards the final exam.

Good luck and remember to check your answers with the solutions provided. If you have any questions, feel free to ask your teacher or refer to the video lessons for more help.

Section A - Multiple Choice Questions

This section contains 40 multiple choice questions. You have 60 minutes to complete it.

Each question has four options labeled A to D. Select the correct answer for each question.

60:00

Question 1

A farmer feeds 20 goats with 500 kg of cassava. How many goats can be fed with 200 kg of cassava?

Question 2

Describe the set of $M = $ {2, 3, 5, 7, 11, 13, 17, 19} in words.

$M = $ {odd numbers less than 20}

$M = $ {factors of 19}

$M = $ {prime numbers less than 20}

$M = $ {whole numbers less than 20}

Question 3

Find the gradient of the line which passes through the points $(2, 3)$ and $(-4, 5)$.

$-3$

-$\dfrac{1}{3}$

$\dfrac{1}{3}$

$3$

Question 4

A trader sold half of a piece of cloth and used two-fifths of the remaining to sew a dress. What fraction of the cloth was left?

$\dfrac{1}{10}$

$\dfrac{3}{10}$

$\dfrac{1}{5}$

$\dfrac{1}{2}$

Question 5

Which of the following inequalities is represented on the number line?

$x < 2$

$x \leq 3$

$x > 3$

$x \geq 2$

Question 6

Ama has 4 one cedi notes and orders ice cream for Gh₵ 1.75 and two toffees at 50 GP each. How much does she have left?

Gh₵ $1.25$

Gh₵ $1.75$

Gh₵ $2.25$

Gh₵ $2.75$

Question 7

The points $M(1, 3)$ and $N(4, 5)$ are in the number plane. Find the vector $\overrightarrow{MN}$

$\begin{pmatrix}3 \\ 2 \end{pmatrix}$

$\begin{pmatrix}-3 \\ -2 \end{pmatrix}$

$\begin{pmatrix}5 \\ 8 \end{pmatrix}$

$\begin{pmatrix}-5 \\ -8 \end{pmatrix}$

Question 8

Solve $2^x = 8 \times 2^0$

$x = 3$

$x = 2$

$x = -2$

$x = -3$

Question 9

Given that $P =$ {4, 8, 12, 16, 20} and $Q =$ {2, 4, 6, 8, 10}, find the product of the members of $(P \cap Q)$.

Question 10

A trader received commission of $5\%$ on goods sold at Gh₵ 25,000.00. Find the commission.

Gh₵ 1,250.00

Gh₵ 1,200.00

Gh₵ 1,100.00

Gh₵ 1,000.00

Question 11

When 0.24 is expressed in the lowest form as $\frac{a}{b}$, the denominator is

125

Question 12

Find the largest value of these numbers: $-1, 0, -6, -3$.

-1

-3

-6

Question 13

Solve: $4x - 2(x + 5) = -10$

$x = -10$

$x = 0$

$\dfrac{1}{2}$

$x = 2$

Question 14

Factorize: $5ay - by + 15a - 3b$

$(y + 3)(5a - b)$

$(y + 5)(3a - b)$

$(y - 3)(5a + b)$

$(y - 5)(3a + b)$

Question 15

Expand and simplify: $2(3a + 1) - 3(4a - 3)$

$11 - 5a$

$11 - 6a$

$11 + 5a$

$11 + 6a$

Question 16

If $a = \begin{pmatrix} -2 \\ 1 \end{pmatrix}$ and $b = \begin{pmatrix} -5 \\ -3 \end{pmatrix}$, find $2a - b$

$\begin{pmatrix} 1 \\ 5 \end{pmatrix}$

\begin{pmatrix} -9 \\ -1 \end{pmatrix}

\begin{pmatrix} 5 \\ 1 \end{pmatrix}

\begin{pmatrix} -1 \\ -1 \end{pmatrix}

Question 17

Charles and Helen started a business with an amount of Gh₵ $7,000.00$. If their contributions were in the ratio $4:3$, respectively, find Helen's contribution.

Gh₵ $2,500.00$

Gh₵ $3,000.00$

Gh₵ $4,000.00$

Gh₵ $5,000.00$

Question 18

A man spends Gh₵ $560.00$ out of his weekly wages of Gh₵ $700.00$ and saves the rest. What percentage did he save?

$10\%$

$15\%$

$20\%$

$25\%$

Question 19

What is the missing number in the sequence: $-5, -2, 1, \dots, 7?$

Question 20

The area of a rectangular card is $15$ cm$^2$. If each side of the card is enlarged by a scale factor of 3, find the area of the enlarged card.

$45$ cm$^2$

$75$ cm$^2$

$90$ cm$^2$

$135$ cm$^2$

Question 21

A rectangular container with dimensions 5 m by 3 m by 4 m is two-third full of water. Find the volume occupied by water in the container.

$50$ m$^3$

$40$ m$^3$

$30$ m$^3$

$20$ m$^3$

Question 22

Solve: $3(x - 5) > 15 - 4(8 - x)$

$x < -32$

$x < -2$

$x < 2$

$x < 32$

Question 23

Ama is three times as old as Kofi. The sum of their ages is 40. How old is Ama?

10 years

30 years

37 years

43 years

Question 24

Express 36 as a product of primes.

$2 \times 3$

$2^2 \times 3^2$

$2^2 \times 3^3$

$2^3 \times 3^2$

Question 25

Esi made sales of 15 twenty cedi notes, 14 ten cedi notes and 15 two cedi notes

Gh₵ 305.00

Gh₵ 440.00

Gh₵ 470.00

Gh₵ 740.00

Question 26

If $2y = 5 - 3x$, find $x$ when $y = 1$.

$-2\dfrac{1}{3}$

$-1$

$0$

$1$

Question 27

A survey shows that 28$\%$ of all men in a village are vegetarian. What is the probability that a man selected at random from the village is a vegetarian?

$\dfrac{7}{25}$

$\dfrac{41}{50}$

$\dfrac{1}{2}$

$1$

Question 28

A box contains 10 green and 8 white balls of the same size. If a ball is selected at random from the box, what is the probability that it is green?

$\dfrac{1}{10}$

$\dfrac{4}{5}$

$\dfrac{5}{9}$

$\dfrac{4}{9}$

Question 29

A boy walked around a circular pond once. If the radius of the pond is 28 m, find the distance covered. [Take $\pi = \frac{22}{7}$]

44 m

88 m

176 m

252 m

Question 30

The population of a town is 56782. What is this number to three significant figures?

567

568

56700

56800

Question 31

How long will the simple interest on Gh₵ 550.00 at 12$\%$ per annum be Gh₵ 132.00?

1 year

2 years

4 years

12 years

Question 32

A point $(-2, 3)$ is reflected in the $x$-axis. Find the image of the point.

$(-3, -2)$

$(-3, 2)$

$(-2, -3)$

$(-2, 3)$

Question 33

Find the rule of the mapping:

$t \rightarrow 10t - 1$

$t \rightarrow 8t + 1$

$t \rightarrow 11t - 2$

$t \rightarrow 7t + 2$

Question 34

Given that $0.03 \times y = 2.4$, find the value of $y$.

0.08

0.8

8.0

80.0

Question 35

Multiply $(8s - 7)$ by $(8s + 7)$

$64s^2 + 49$

$64s^2 - 49$

$16s^2 - 42$

$16s^2 + 42$

Question 36

Anowa scored an average of 53 in Science and Mathematics. If she scored 50 and 60 in English Language and Social Studies respectively, find her mean score in all the four subjects.

Question 37

Mr Adu bought 400 bags of maize for his farm animals. If he used 120 bags to feed the animals, find the percentage of the maize left.

70$\%$

60$\%$

50$\%$

40$\%$

Question 38

Two interior angles of a triangle are $(3x - 10)^\circ$ and $(4x + 20)^\circ$. Find an expression for the third angle.

$(170 - 7x)^\circ$

$(150 - 5x)^\circ$

$(120 - 7x)^\circ$

$(100 - 5x)^\circ$

Question 39

In an examination, Abu answered nine questions in 2 hours. He spent 20 minutes on the first question and the same time on each of the remaining questions. How many minutes did he spend on each of the other questions?

8.0 minutes

10.0 minutes

12.0 minutes

12.5 minutes

Question 40

It costs a carpenter Gh₵ 25.00 to make a chair. How much should it be sold to make a profit of 40$\%$?

Gh₵ 15.00

Gh₵ 35.00

Gh₵ 40.00

Gh₵ 50.00

Section B

Question 1

Given that $P = $ {multiples of $3$} and $Q = $ {positive even numbers} are subsets of $\mu = $ {$x: 1 < x \leq 20$, where $x$ is a counting number}:

(i) list the elements in $P \cap Q$;

(ii) list all the subsets in $P \cap Q$.

Solution

$\mu = $ {$x: 1 < x \leq 20$, where $x$ is a counting number}

$\Rightarrow \mu = $ {$2, 3, 4, 5, ..., 20$}

$P = $ {multiples of $3$}

$\Rightarrow$ $P = $ {3, 6, 9, 12, 15, 18}

$Q = $ {positive even numbers}

$\Rightarrow Q = $ {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}

(i) $P \cap Q$

$\Rightarrow$ {6, 12, 18}

(ii) Subsets of $P \cap Q$

$\Rightarrow$ { }, {6}, {12}, {18}, {6, 12}, {6, 18}, {12, 18}, {6, 12, 18}

If $\dfrac{1}{y} = 3k - \dfrac{2}{x}$,

(i) make $y$ the subject of the relation.

(ii) using the result in ($b$)(i), find the value of $y$ when $x = -1$ and $k = 2$.

Solution

$\dfrac{1}{y} = 3k - \dfrac{2}{x}$

(i) Making $y$ the subject:

$\Rightarrow \dfrac{1}{y} = \dfrac{x(3k) - 2}{x}$

$\Rightarrow \dfrac{1}{y} = \dfrac{3kx - 2}{x}$

Cross multiplying:

$\Rightarrow y(3kx - 2) = x$

$\Rightarrow \dfrac{y(3kx - 2)}{3kx - 2} = \dfrac{x}{3kx - 2}$

$\Rightarrow y = \dfrac{x}{3kx - 2}$

(ii) when $x = -1$ and $k = 2$

$\Rightarrow y = \dfrac{-1}{3(2)(-1) - 2}$

$\Rightarrow y = \dfrac{-1}{-6 - 2}$

$\Rightarrow y = \dfrac{-1}{-8}$

$\Rightarrow y = \dfrac{1}{8}$

$\therefore$ when $x$ is -1 and $k$ is 2, $y$ is $\frac{1}{8}$

Question 2

Evaluate $\dfrac{4000 \times 0.35}{0.05}$, leaving the answer in standard form.

Solution

$\dfrac{4000 \times 0.35}{0.05}$

$\Rightarrow \dfrac{(4 \times 10^3) \times (35 \times 10^{-2})}{5 \times 10^{-2}}$

$\Rightarrow \dfrac{4 \times 10^3 \times 35}{5}$

$\Rightarrow 4 \times 10^3 \times 7$

$\Rightarrow 28 \times 10^3$

$\Rightarrow 2.8 \times 10^1 \times 10^3$

$\Rightarrow 2.8 \times 10^{1+3}$

$\Rightarrow 2.8 \times 10^4$

Mr Boakye gets $10\%$ commission on type $P$ house he sells and $15\%$ on type $Q$ house. He sells 3 type $P$ houses at Gh₵ $700,000.00$ each and 4 type $Q$ at Gh₵ $1,400,000.00$ each. Calculate the total commission he makes.

Solution

Cost of type $P$ house $\Rightarrow$ Gh₵ $700,000.00$

Number of type $P$ houses sold $\Rightarrow 3$

Total amount received for type $P$:
$\Rightarrow 3 \times 700,000$
$\Rightarrow$ Gh₵ $2,100,000$

Commision on type $P$:
$\Rightarrow 10\%$ of $2,100,000$
$\Rightarrow$ Gh₵ $210,000$

Cost of type $Q$ house $\Rightarrow$ Gh₵ $1,400,000.00$

Number of type $Q$ houses sold $\Rightarrow 4$

Total amount received for type $Q$:
$\Rightarrow 4 \times 1,400,000$
$\Rightarrow$ Gh₵ $5,600,000$

Commision on type $Q$:
$\Rightarrow 15\%$ of $5,600,000$
$\Rightarrow$ Gh₵ $840,000$

Total commision received:

$\Rightarrow$ $210,000 + 840,000$

$\Rightarrow$ Gh₵ $1,050,000$

$\therefore$ the total commission received for type P and type Q is Gh₵ 1,050,000

Question 3

Given that $a = \begin{pmatrix} 2 \\ 3 \end{pmatrix}$, $b = \begin{pmatrix} x \\ -3 \end{pmatrix}$ and $c = \begin{pmatrix} 7 \\ 3 \end{pmatrix}$, find:

(i) the value of $x$, if $2a + b = c$;

(ii) $d = c - 3a$;

(iii) $|d|$

Solution

$a = \begin{pmatrix} 2 \\ 3 \end{pmatrix}$, $b = \begin{pmatrix} x \\ -3 \end{pmatrix}$ $c = \begin{pmatrix} 7 \\ 3 \end{pmatrix}$

(i) $2a + b = c$

$\Rightarrow 2\begin{pmatrix} 2 \\ 3 \end{pmatrix} + \begin{pmatrix} x \\ -3 \end{pmatrix} = \begin{pmatrix} 7 \\ 3 \end{pmatrix}$

$\Rightarrow \begin{pmatrix} 4 \\ 6 \end{pmatrix} + \begin{pmatrix} x \\ -3 \end{pmatrix} = \begin{pmatrix} 7 \\ 3 \end{pmatrix}$

Equating the $x$ components:

$\Rightarrow 4 + x = 7$

$\Rightarrow \hspace{0.85cm} x = 7 - 4$

$\Rightarrow \hspace{0.85cm} x = 3$

$\therefore$ $x$ is 3

(ii) $d = c - 3a$

$\Rightarrow d = \begin{pmatrix} 7 \\ 3 \end{pmatrix} - 3\begin{pmatrix} 2 \\ 3 \end{pmatrix}$

$\Rightarrow d = \begin{pmatrix} 7 \\ 3 \end{pmatrix} - \begin{pmatrix} 6 \\ 9 \end{pmatrix}$

$\Rightarrow d = \begin{pmatrix} 7 - 6 \\ 3 - 9 \end{pmatrix}$

$\Rightarrow d = \begin{pmatrix} 1 \\ -6 \end{pmatrix}$

(iii) $|d|$

$\Rightarrow \sqrt{(1)^2 + (-6)^2}$

$\Rightarrow \sqrt{1 + 36}$

$\Rightarrow \sqrt{37}$ units

A Polytank contains $4500$ litres of water and $\dfrac{1}{5}$ of the water is used for cleaning.

(i) Find the volume of water used for cleaning.

(ii) What percentage of water is left in the tank?

Solution

Volume of water $= 4500$ litres

(i) Volume used for cleaning

$\Rightarrow \dfrac{1}{5} \times 4500$ litres

$\Rightarrow 900$ litres

$\therefore 900$ litres of water was used for cleaning.

(ii) Volume left in tank:

$\Rightarrow$ Total volume $-$ volume used for cleaning

$\Rightarrow 4500 - 900$

$\Rightarrow 3600$ litres

Percentage of water left:

$\Rightarrow \dfrac{\text{volume left}}{\text{Total volume}} \times 100\%$

$\Rightarrow \dfrac{3600}{4500} \times 100\%$

$\Rightarrow \dfrac{36}{45} \times 100\%$

$\Rightarrow \dfrac{4 \times 9}{5 \times 9} \times 100\%$

$\Rightarrow \dfrac{4}{5} \times 100\%$

$\Rightarrow 4 \times 20\%$

$\Rightarrow 80\%$

$\therefore$ 80% of water is left in the tank.

Question 4

A woman borrowed Gh₵ $5,300.00$ to pay for her child's university fees. If she borrowed at a rate of $8\%$ simple interest per annum for 9 months, find the interest paid.

Solution

Principal, $P =$ Gh₵ $5,300.00$

Rate, $R = 8\%$

Time, $T = 9$ months

$\Rightarrow T = \frac{9}{12} = \frac{3}{4}$

Interest, $I = \dfrac{P \times R \times T}{100}$

Interest, $I = \dfrac{5,300 \times 8 \times \frac{3}{4}}{100}$

Interest, $I = \dfrac{5,300 \times 2 \times 3}{100}$

Interest, $I = 53 \times 6$

Interest, $I =$ Gh₵ $318.00$

$\therefore$ the interest paid was Gh₵ $318.00$

A father shared his piece of land to his three children. The first child had $\frac{2}{5}$ of the land and the second had $5$ acres more than the first. If the third child had $20$ acres, find how many acres of land the:

(i) father shared;

Solution

(i) let $x =$ the total acres of land shared

$\Rightarrow$ First child's share $= \frac{2}{5}x$

$\Rightarrow$ Second child's share $= \frac{2}{5}x + 5$

Third child's share $= 20$

$\Rightarrow x = \frac{2}{5}x + \left(\frac{2}{5}x + 5\right) + 20$

$\Rightarrow x = \frac{2}{5}x + \frac{2}{5}x + 5 + 20$

$\Rightarrow x = \frac{4}{5}x + 25$

$\Rightarrow 5x = 4x + 5(25)$

$\Rightarrow 5x - 4x = 125$

$\Rightarrow x = 125$ acres

$\therefore$ the total land shared by the father was 125 acres.

(ii) first child received;

(iii) second child received.

Solution

(ii) First child's share:

$\Rightarrow \dfrac{2}{5}x$

$\Rightarrow \dfrac{2}{5} \times 125$

$\Rightarrow 2 \times 25$

$\Rightarrow 50$ acres

$\therefore$ the first child received 50 acres.

(iii) The second child's share:

$\Rightarrow \dfrac{2}{5}x + 5$

$\Rightarrow \left(\dfrac{2}{5} \times 125\right) + 5$

$\Rightarrow \left(2 \times 25\right) + 5$

$\Rightarrow 50 + 5$

$\Rightarrow 55$ acres

$\therefore$ the second child received 55 acres.

Question 5

The pie chart shows the weight (in kg) of items Mrs. Mensah bought for her household.

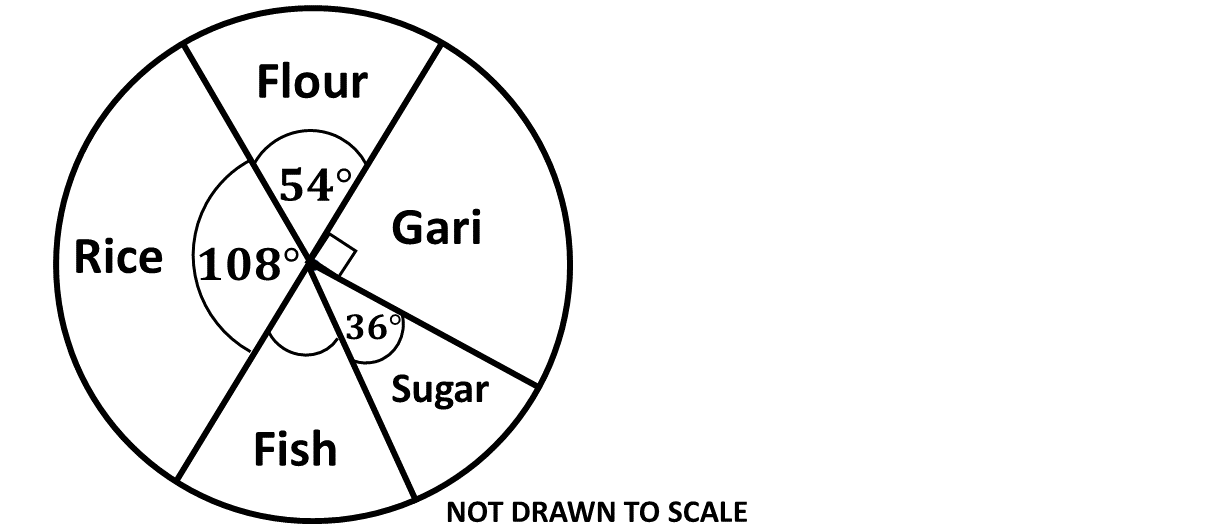
(i) What angle represents fish?

(ii) If she bought a total of 20 kg of items,
($\alpha$) what is the weight of flour bought?
($\beta$) express, correct to one decimal place, the weight of sugar as a percentage of the weight of rice.

Solution

(i) let $x =$ angle of sector for Fish

$\Rightarrow 360^\circ = x + 36^\circ + 90^\circ + 54^\circ + 108^\circ$

$\Rightarrow 360^\circ = x + 288^\circ$

$\Rightarrow 360^\circ - 288^\circ = x $

$\Rightarrow x = 72^\circ $

$\therefore$ the angle representing fish is 72°

(ii) total weight $= 20$ kg

($\alpha$) angle of sector for flour $= 54^\circ$

Weight of flour:

$\Rightarrow \dfrac{\text{angle for flour}}{\text{total angle}} \times \text{total weight}$

$\Rightarrow \dfrac{54^\circ}{360^\circ} \times 20$ kg

$\Rightarrow \dfrac{3 \times 18}{20 \times 18} \times 20$ kg

$\Rightarrow \dfrac{3}{20} \times 20$ kg

$\Rightarrow 3$ kg

$\therefore$ the weight of flour bought was 3 kg

($\beta$)

Angle of sector for sugar $ = 36^\circ$

Angle of sector for rice $ = 108^\circ$

Weight of sugar as percentage of weight of rice:

$\Rightarrow \dfrac{36^\circ}{108^\circ} \times 100\%$

$\Rightarrow \dfrac{1 \times 36}{3 \times 36} \times 100\%$

$\Rightarrow \dfrac{1}{3} \times 100\%$

$\Rightarrow \dfrac{100}{3}\%$

$\Rightarrow 33.3\%$

$\therefore$ the weight of sugar as a percentage of weight of rice is 33.3%

In a class of 30 students, five wear glasses. If a student is selected at random from the class, what is the probability that the student does not wear glasses?

Solution

Total students in the class $= 30$

Students wearing glasses $= 5$

Students not wearing glasses:

$\Rightarrow 30 - 5$

$\Rightarrow 25$

Probability $= \dfrac{\text{successful outcomes}}{\text{total outcomes}}$

Probability (student not wearing glasses):

$\Rightarrow \dfrac{25}{30}$

$\Rightarrow \dfrac{5 \times 5}{6 \times 5}$

$\Rightarrow \dfrac{5}{6}$

$\therefore$ the probability of selecting a student not wearing glasses is $\frac{5}{6}$

Question 6

Adamu was travelling a distance of $40$ km from Kadumgu to Datanu. Sixty minutes after starting the journey, he made a stop at Cooltown, $10$ km from Kadumgu to rest for $30$ minutes. He then continued the journey from Cooltown and reached Datanu 60 minutes later.

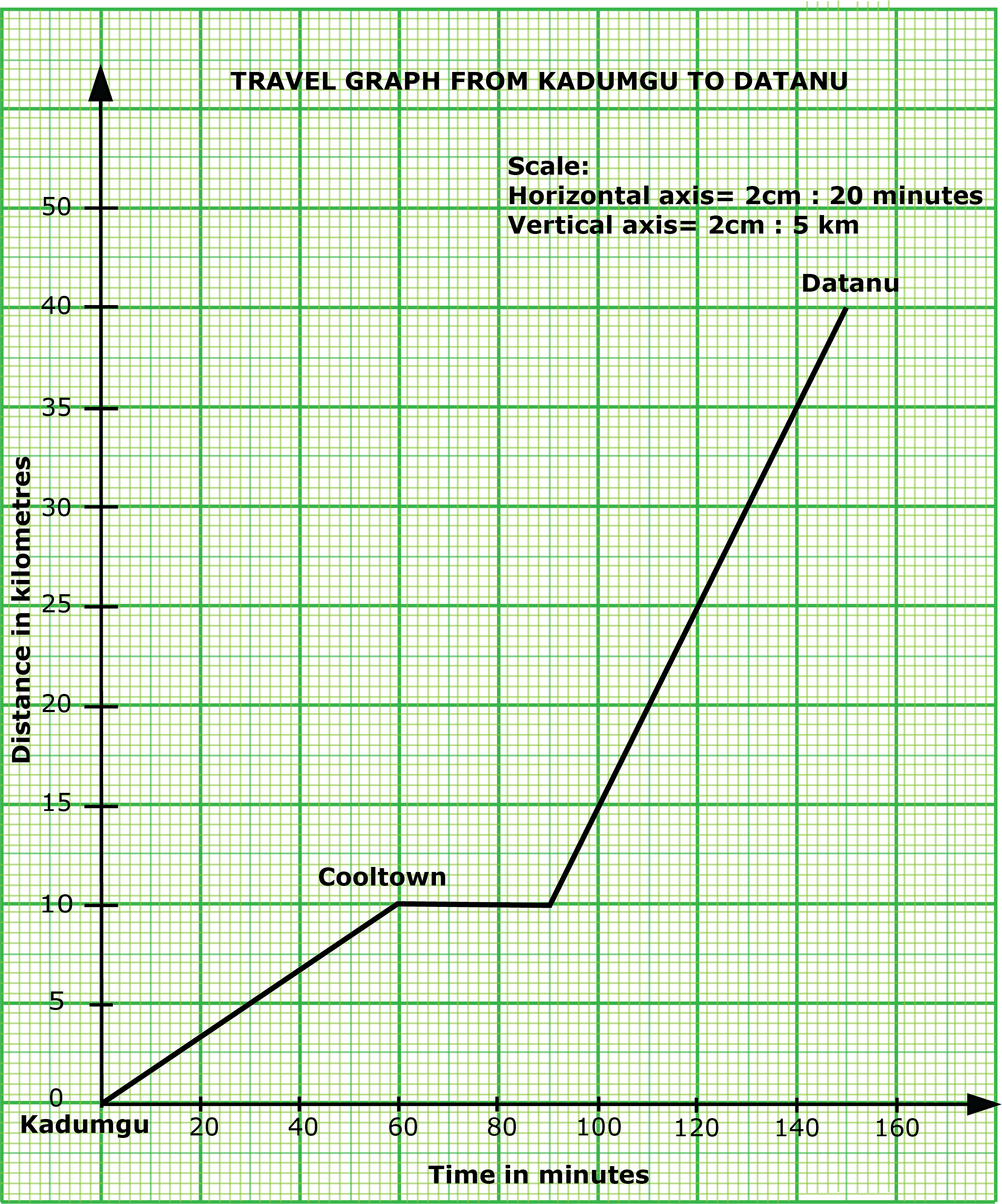
Using a scale of 2 cm to 20 minutes on the horizontal axis and 2 cm to 5 km on the vertical axis, draw a distance-time graph for Adamu's journey.
Use the graph to determine the:

(i) distance from Cooltown to Datanu;

(ii) total time (in minutes), taken by Adamu to make the whole journey including the rest time;

(iii) average speed of Adamu from Cooltown to Datanu.
If Adamu did not rest but travelled to Datanu within the time, what was his average speed?

Solution

($a$)

($b$)

(i) distance from Cooltown to Datanu:

From the graph, distance from Cooltown to Datanu is 30 km

(ii) total time taken:

From the graph, the total time taken is 150 minutes.

$\Rightarrow 2$ hours $30$ minutes.

(iii) From Cooltown to Datanu:

distance $= 30$ km

time $= 60 \ \text{mins}$

time $= 1 \ \text{hr}$

speed $= \dfrac{\text{distance}}{\text{time}}$

speed $= \dfrac{30 \ \text{km}}{1 \ \text{hr}}$

speed $= 30 \ \text{km}/ \text{h}$

($c$)

distance $= 40$ km

time taken (without rest) $= 2 \ \text{hr}$

speed $= \dfrac{40 \ \text{km}}{2 \ \text{hr}}$

speed $= 20$ km/h

$\therefore$ the average speed is 20 km/h.

GUIDE (BECE - 2025)

Section A - Multiple Choice Questions

Your Test Results

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Question 9

Question 10

Question 11

Question 12

Question 13

Question 14

Question 15

Question 16

Question 17

Question 18

Question 19

Question 20

Question 21

Question 22

Question 23

Question 24

Question 25

Question 26

Question 27

Question 28

Question 29

Question 30

Question 31

Question 32

Question 33

Question 34

Question 35

Question 36

Question 37

Question 38

Question 39

Question 40

Section B

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6