BECE 2022 | JHS Mathematics | The Let's Learn Project

GUIDE (BECE - 2022)

You have 60 minutes for each section. Try to work on your speed as you prepare towards the final exam.

Good luck and remember to check your answers with the solutions provided. If you have any questions, feel free to ask your teacher or refer to the video lessons for more help.

Section A - Multiple Choice Questions

This section contains 40 multiple choice questions. You have 60 minutes to complete it.

Each question has four options labeled A to D. Select the correct answer for each question.

60:00

Question 1

Write 1930.54 in standard form.

$1.93054 \times 10^2$

$1.93054 \times 10^3$

$1.93054 \times 10^{-2}$

$1.93054 \times 10^{-3}$

Question 2

For what value of $x$ is $3^x = 81$?

$2$

$4$

$27$

$9$

Question 3

A car travels 36 kilometers in an hour. Find it's speed in meters per second.

$10$ ms$^{-1}$

$100$ ms$^{-1}$

$20$ ms$^{-1}$

$200$ ms$^{-1}$

Question 4

If $\dfrac{n}{100} = 10.5$ find the value of $n$.

$1050$

$0.105$

$105$

$0.0105$

Question 5

If a trader made a profit of 10$\%$ in selling a shirt for Gh₵ 44.00, find the cost price.

Gh₵ $39.60$

Gh₵ $38.50$

Gh₵ $48.40$

Gh₵ $40.00$

Question 6

Simplify $1\dfrac{1}{5} \div 2\dfrac{1}{10}$

$\dfrac{4}{7}$

$2\dfrac{13}{25}$

$\dfrac{12}{63}$

$\dfrac{25}{63}$

Question 7

The volume of a cylinder is $40 \pi$ cm$^3$. If the height of the cylinder is 10 cm, find the base radius.

$1$ cm

$4$ cm

$3$ cm

$2$ cm

Question 8

The longest chord of a circle is the

sector

segment

circumference

diameter

Question 9

If $x = \dfrac{b^2 - 4ac}{2a}$, find $x$ when $a = 2$, $b = -4$ and $c = -2$.

$16$

$0$

$4$

$8$

Question 10

The ratio of farmers to children in a village is $13:11$. If there were 312 farmers in the village, how many children were there?

$143$

$169$

$264$

$48$

Question 11

Arrange the following fractions from the lowest to the highest:

$\dfrac{2}{3}, \dfrac{1}{4}, \dfrac{3}{5}$

$\dfrac{2}{3}, \dfrac{3}{5}, \dfrac{1}{4}$

$\dfrac{1}{4}, \dfrac{3}{5}, \dfrac{2}{3}$

$\dfrac{3}{5}, \dfrac{1}{4}, \dfrac{2}{3} $

Question 12

What is the length of the side of a square of area $225$ cm$^2$?

$15$ cm

$56.25$ cm

$12.00$ cm

$112.50$ cm

Question 13

The rule of a mapping is $x \rightarrow 2x^2 - 1$. What number does $2$ map to?

$3$

$9$

$7$

$8$

Question 14

Express $108$ as a product of prime factors.

$2^3 \times 3$

$2 \times 3^4$

$2^3 \times 3^2$

$2^2 \times 3^3$

Question 15

Express $15 : 12$ in the $1 : n$.

$1 : 12$

$1 : 15$

$1 : 1.2$

$1 : 0.8$

Question 16

Given that $P(3, -2)$ and $Q(-2, 4)$ are points in a plane, find the gradient of the line joining $P$ to $Q$.

$\dfrac{5}{6}$

$-\dfrac{5}{6}$

$-\dfrac{6}{5}$

$\dfrac{6}{5}$

Question 17

A shop is rented at Gh₵ $9.00$ per month. How much money is paid in $1\frac{1}{2}$ years?

Gh₵ $162.00$

Gh₵ $13.50$

Gh₵ $135.00$

Gh₵ $6.00$

In the diagram, $AB$ is parallel to $DE$, $\angle ABC = 81^\circ$ and $\angle DCE = 20^\circ$.
Use the information to answer questions 18 and 19

Question 18

What is the value of $x$?

$20^\circ$

$101^\circ$

$81^\circ$

$61^\circ$

In the diagram, $AB$ is parallel to $DE$, $\angle ABC = 81^\circ$ and $\angle DCE = 20^\circ$.
Use the information to answer questions 18 and 19

Question 19

Find the value of $y$.

$101^\circ$

$20^\circ$

$79^\circ$

$81^\circ$

Question 20

What is the probability that a number greater than 5 shows up when a die is thrown?

$\dfrac{1}{6}$

$\dfrac{1}{3}$

$\dfrac{5}{6}$

$\dfrac{2}{3}$

Question 21

A mother has Gh₵ $5.00$ and gives each of her 3 children Gh₵ $1.50$ as pocket money.

Gh₵ $4.50$

Gh₵ $0.50$

Gh₵ $0.15$

Gh₵ $3.50$

Question 22

Expand: $(2a - b)(a - b)$

$2a^2 - 3ab - b^2$

$2a^2 + 3ab + b$

$2a^2 - 3ab + b^2$

$2a^2 + 3ab - b$

Question 23

Peter had Gh₵ $200.00$ and spent Gh₵ $83.00$. What percentage of the money is left?

$29.06 \%$

$70.94 \%$

$41.50 \%$

$58.50 \%$

The stem and leaf plot shows the weight (kg) of cocoa bags weighed in a week.
Use the information to answer questions 24 to 26.

Question 24

What is the modal weight of the bags of cocoa?

$60$ kg

$68$ kg

$65$ kg

$64$ kg

The stem and leaf plot shows the weight (kg) of cocoa bags weighed in a week.
Use the information to answer questions 24 to 26.

Question 25

What is the median weight of the bags of cocoa?

$65$ kg

$62$ kg

$61$ kg

$68$ kg

The stem and leaf plot shows the weight (kg) of cocoa bags weighed in a week.
Use the information to answer questions 24 to 26.

Question 26

How many bags of cocoa were weighed in the week?

$41$

$35$

$29$

$6$

Question 27

Simplify: $- 15 - (-20) + (-10)$

$-45$

$-25$

$-5$

$5$

Question 28

Given that $\overrightarrow{PQ} = \begin{pmatrix} -3 \\ 8 \end{pmatrix}$, find $\overrightarrow{QP}$.

$\begin{pmatrix} -3 \\ 8 \end{pmatrix}$

$\begin{pmatrix} -3 \\ -8 \end{pmatrix}$

$\begin{pmatrix} 8 \\ -3 \end{pmatrix}$

$\begin{pmatrix} 3 \\ -8 \end{pmatrix}$

Question 29

Which of the following is not a quadrilateral?

Parallelogram

Rhombus

Triangle

Rectangle

Question 30

Express $\frac{3}{8}$ as a decimal fraction.

$0.429$

$0.375$

$0.625$

$0.365$

Question 31

Factorize completely: $xy - xm - my + m^2$

$(y - m)(m - x)$

$(m - y)(m - x)$

$(x - m)(y - m)$

$(m - y)(x - m)$

Question 32

Adwoa travelled 12 km due north and 5 km due east. How far was she from her starting point?

13 km

7 km

17 km

60 km

Question 33

A certain number is subtracted from 12 and the result is multiplied by 3. If the answer is 21, find the number.

$4$

$8$

$6$

$5$

Question 34

A football match starts at 2.20 pm and lasts for 1 hour 50 minutes. At what time will the game end?

3.10 pm

5.10pm

4.10 pm

6.10pm

Question 35

Given that $117(12 + 18) = 117(15 + k)$, find the value of $k$.

$-30$

$30$

$15$

$-15$

Question 36

If $a = \begin{pmatrix} 2 \\ -3 \end{pmatrix}$ and $b = \begin{pmatrix} -2 \\ 3 \end{pmatrix}$, find $a + b$.

$\begin{pmatrix} 4 \\ 0 \end{pmatrix}$

$\begin{pmatrix} 2 \\ 3 \end{pmatrix}$

$\begin{pmatrix} 0 \\ 0 \end{pmatrix}$

$\begin{pmatrix} 0 \\ 6 \end{pmatrix}$

Question 37

Solve $(x - 1) = \frac{1}{2}(x + 2)$

$1\frac{1}{3}$

$0$

$1\frac{1}{2}$

$4$

Question 38

The point $S(4, 3)$ is reflected in the y-axis. Find the coordinates of the image of $S$.

$(-3, 4)$

$(3, -4)$

$(-4, 3)$

$(4, -3)$

Question 39

Solve $5x - (7x - 3) \leq 9$.

$x \geq -3$

$x \leq 3$

$x \geq -6$

$x \leq -6$

Question 40

Which of the following is the largest set?

Natural numbers

Composite numbers

Integers

Whole numbers

Section B

Question 1

Given that $P =$ {factors of 36} and $Q =$ {factors of 54},

$(i)$ List the members in the sets $P$ and $Q$.

$(ii)$ Find:

$\hspace{0.5cm}$ A. $P \cap Q$

$\hspace{0.5cm}$ B. $n(P \cap Q)$

$\hspace{0.5cm}$ Γ. The Highest Common Factor (HCF) of 36 and 54.

Solution

Question 1 $(i)$

$P =$ {factors of 36}

$\Rightarrow P =$ {1, 2, 3, 4, 6, 9, 12, 18, 36}

$Q =$ {factors of 54}

$\Rightarrow Q =$ {1, 2, 3, 6, 9, 18, 27, 54}

Question 1 $(ii)$

$\hspace{0.5cm}$ A. $P \cap Q =$ {1, 2, 3, 6, 9, 18}

$\hspace{0.5cm}$ B. $n(P \cap Q) = 6$

$\hspace{0.5cm}$ Γ. The Highest Common Factor (HCF) of 36 and 54:

$\hspace{0.8cm}$ Common factors of 36 and 54 $\Rightarrow$ {1, 2, 3, 6, 9, 18}

$\hspace{0.8cm}$ Highest common factor $\Rightarrow 18$

$\hspace{0.8cm} \therefore$ the highest common factor of 36 and 54 is 18.

Write down the next two terms of the sequence 1, 4, 9, ..., ...

Solution

The median of the ordered set of observations 2, 3, (4$m$-3),(3$m$+1), 11 and 13 in ascending order is 6. Find the value of m.

Solution

Question 2

Simplify: $(\frac{1}{3} + \frac{1}{12}) \div (\frac{2}{3} - \frac{5}{8})$

Solution

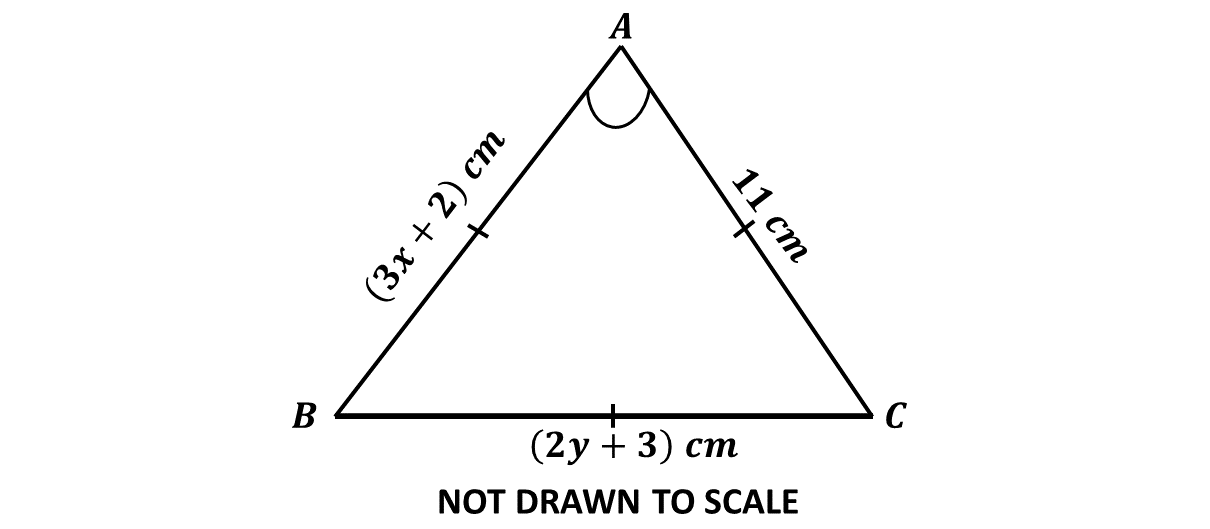
Find the product of $(2x - 3)$ and $(2x + 3)$.

Solution

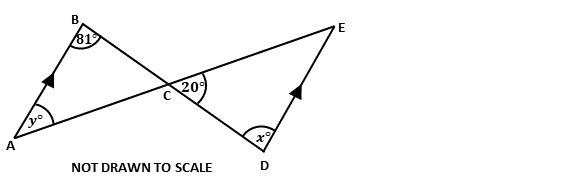
In the diagram, $ABC$ is an equilateral triangle. Find the value of $(x + y)$.

Solution

Question 3

Given the relation $L = \dfrac{2(m^2 - n^2)}{4(m + n)}$

$(i)$ simplify $L$:

$(ii)$ find the value of $L$ when $m = 2$ and $n = 3$.

Solution

Solve $\dfrac{4}{3x} = 7 - \dfrac{3}{x}$

Solution

A salesman gets a commission of $5\frac{1}{2}\%$ of the value of items he sells. The salesman sells 12 textbooks at GH₵ 25.00 per book, 3 scientific calculators at GH₵ 50.00 per calculator and 8 packets of bic pens at GH₵ 50.00 per packet. Calculate the salesman's commission.

Solution

Question 4

Fred is $(x - 1)$ years old now. How old:

$(i)$ was he 4 years ago?

$(ii)$ will he be 8 years from now?

$(iii)$ is he now, if his age in 8 years time will be three times his age 4 years ago?

Solution

The perimeter of a rectangular cocoa farm is 497 km. The length of the farm is $2\frac{1}{2}$ times the width. Find the:

$(i)$ width;

$(ii)$ length of the farm.

Solution

Question 5

Factorize: $(x-y)(3m+n)-(x-y)(m-2n)$

Solution

Given that $\mathbf{p} = \begin{pmatrix} 2 - 3x\\5 - 2y \end{pmatrix}, \ \mathbf{q} = \begin{pmatrix} -1\\5 \end{pmatrix}$ and $\mathbf{p} - \mathbf{q} = \begin{pmatrix} 6\\8 \end{pmatrix}$.

Find the value of $(x + y)$.

Solution

$\hspace{0.5cm} (i)$ Find the truth set of $\dfrac{x - 1}{2} \leq \dfrac{1}{2} + x$

$\hspace{0.5cm} (ii)$ Illustrate the answer in $(i)$ on the number line.

Solution

Question 6

Copy and complete the table for the relation $y = 5 - 2x$ for $-3 \leq x \leq 4$

Solution

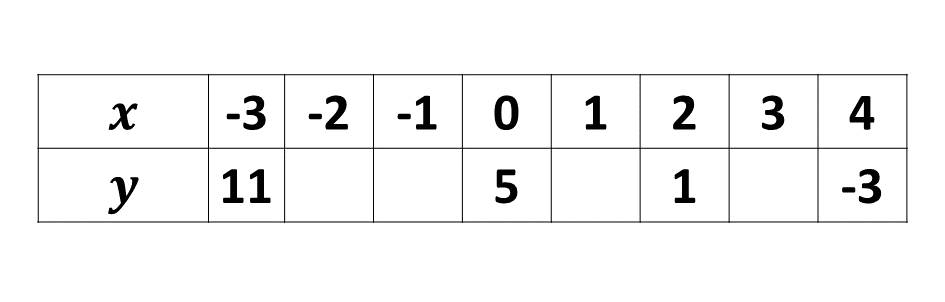
Using a scale of 2 cm to 1 unit on the $x$ - axis and 2 cm to 2 units on the $y$ - axis, draw on a graph sheet two perpendicular axes $Ox$ and $Oy$ for $-5 \leq x \leq 5$ and $-12 \leq y \leq 12$.

Solution

$\hspace{0.5cm} (i)$ Using the table, plot all the points of the relation $y = 5 - 2x$.

$\hspace{0.5cm} (ii)$ Draw a straight line through all the points.

Solution

Using the graph, find the:

$\hspace{0.5cm} (i)$ value of $y$ when $x = -2.6$;

$\hspace{0.5cm} (ii)$ value of $x$ when $y = -2.8$;

$\hspace{0.5cm} (iii)$ gradient of the line.

Solution

GUIDE (BECE - 2022)

Section A - Multiple Choice Questions

Your Test Results

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8

Question 9

Question 10

Question 11

Question 12

Question 13

Question 14

Question 15

Question 16

Question 17

Question 18

Question 19

Question 20

Question 21

Question 22

Question 23

Question 24

Question 25

Question 26

Question 27

Question 28

Question 29

Question 30

Question 31

Question 32

Question 33

Question 34

Question 35

Question 36

Question 37

Question 38

Question 39

Question 40

Section B

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6