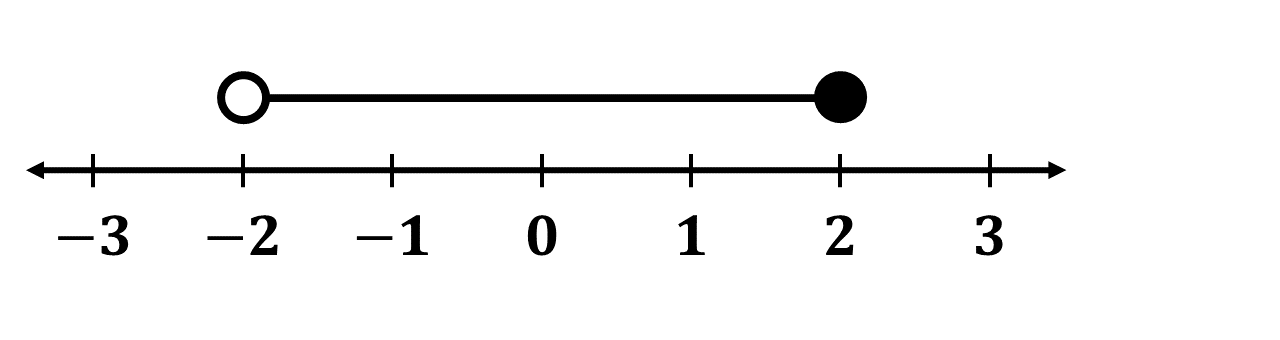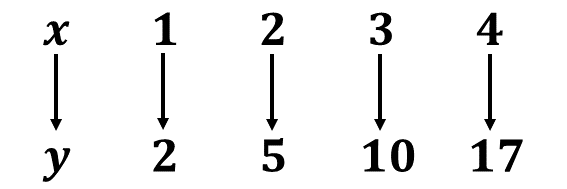GUIDE (BECE - 2020)
You have 60 minutes for each section. Try to work on your speed as you prepare towards the final exam.
Good luck and remember to check your answers with the solutions provided. If you have any questions, feel free to ask your teacher or refer to the video lessons for more help.
Section A - Multiple Choice Questions
This section contains 40 multiple choice questions. You have 60 minutes to complete it.
Each question has four options labeled A to D. Select the correct answer for each question.
Section B
Question 1
-
If \(M =\) {Prime integers between \(1\) and \(11\)} and \(N =\) {factors of 12}, find:
\((i)\) \(M \cup N\)
\((ii)\) \(M \cap N\)
- Simplify \(45 \div 3 + 2 \times 8 - 12 + 42\)
-
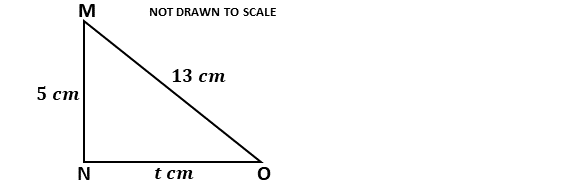
Solution
Solution
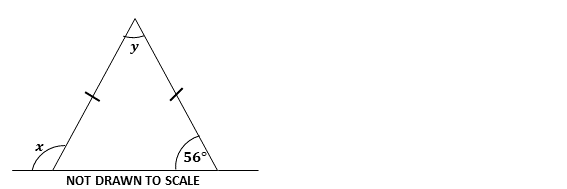
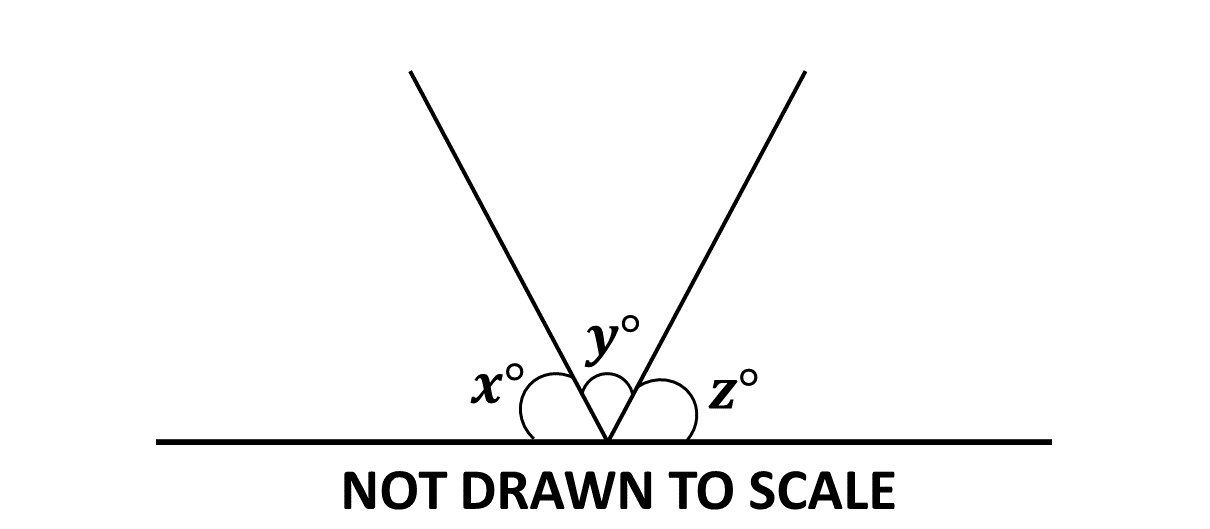
In the diagram, \(x, y\) and \(z\) are angles on a straight line. If \(x^\circ : z^\circ = 2 : 3\), and \(y = 80^\circ\), find \(x\).
Solution
Question 2
-
Simplify: \(5(6 - ab) + 2(-7 + 3ab)\)
-
The equation of a straight line is given by \(3x - 2y - 6 = 0\). Find the:
\((i)\) gradient of the line;
\((ii)\) y-intercept.
-
Adwoa received a commission of 20% on bread she sold. In one week, Adwoa's commission was Gh₵ 540.00.
\((i)\) How much bread did she sell during that week?
\((ii)\) Find her average daily commission.
Solution
Solution
Solution
Question 3
-
Express \(\left(\dfrac{13}{15} - \dfrac{7}{10}\right)\) as a percentage.
-
Factorize: \(ay - y - a + 1\).
-
In a fishing community of 9,400 people, the number of women exceeds the number of men by 1,500. Find the ratio of men to women in the community.
Solution
Solution
Solution
Question 4
-
Solve: \(\dfrac{2x + 3}{3} + 2x = 10\)
-
Multiply 0.03858 by 0.02, leaving the answer in standard form.
-
A cylindrical container of height 28 cm and diameter 18 cm is filled with water. The water is then poured into another container with a rectangular base of length 27 cm and width 11 cm. Calculate the depth of the water in the container. [Take \(π = \frac{22}{7}\)]
Solution
Solution
Solution
Question 5
-
If \(11y = (18)^2 - (15)^2\), find the value of \(y\).
-
Find the perimeter of a circle with radius 35 cm. [Take \(\pi = \frac{22}{7}\)]
-
Given that \(m = \dfrac{r - s}{2nr}\)
\((i)\) make \(r\) the subject of the relation.
\((ii)\) find the value of \(r\) when \(s = 117, m = 2\) and \(n = -3\).
Solution
Solution
Solution
Question 6
-
Copy and complete the table for the relation \(y = 12x - 9\)
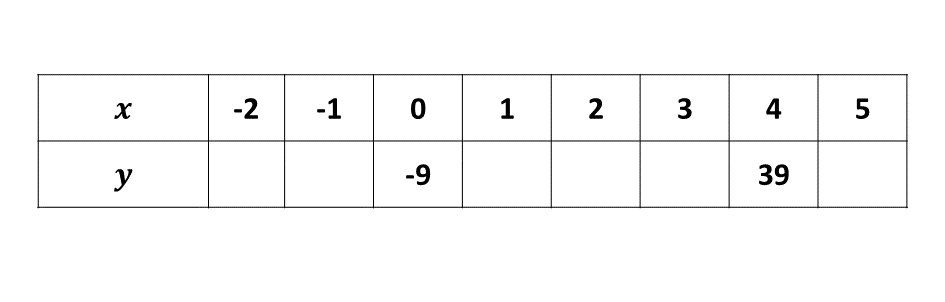
\((i)\) Using a scale of 2 cm to 1 unit on the \(x\) - axis and 2 cm to 10 units on the \(y\) - axis, draw on a graph sheet two perpendicular axes \(Ox\) and \(Oy\).
\((ii)\) Using the table, plot all the points of the relation \(y = 12x - 9\) on the graph.
\((iii)\) Draw a straight line through the points.
\((iv)\) Use the graph to find:
\(\hspace{0.5cm} (\alpha)\) \(y\) when \(x = 2.5\);
\(\hspace{0.5cm} (\beta)\) \(x\) when \(y = 10\);
-
List the integers within the interval \(7 < x \leq 14\)
Solution
Solution